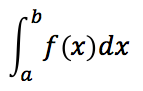
SUNY Geneseo Department of Mathematics
Math 303
Fall 2015
Prof. Doug Baldwin
Complete by Tuesday, September 22
Grade by Thursday, September 24
This problem set reinforces your ability to mathematically analyze the execution time of iterative algorithms, and also develops your understanding of asymptotic notation.
This problem set is based on material in sections 2.2 and 3.1 of our textbook. We discussed (or will discuss) this material in lectures between September 8 and September 15.
Solve each of the following problems.
(Based on Exercise 2.2-3 in our textbook.) Sequential Search is a simple algorithm for searching a list a of length n to see if it contains a value x. Sequential Search returns true if a contains x, and false if it does not. Here is pseudocode for Sequential Search:
search( a1..n, x )
for i = 1 to n
if ai = x
return true
end of for
return falseDerive the best- and worst-case execution times of Sequential Search as functions of list length. Express your times in asymptotic notation, giving them in the tightest form (e.g., Θ, O, or Ω) supported by your analysis.
Consider evaluating the definite integral
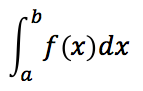
Perhaps the simplest way to evaluate such an integral computationally is as a Riemann sum, i.e., split the interval from a to b into n sub-intervals, define rectangles in each sub-interval whose widths are (b-a)/n and whose heights come from values of f in each interval, and then add up the areas of all the rectangles. In pseudocode this algorithm looks like this:
integrate( f, a, b, n )
deltaX = ( b - a ) / n // Width of sub-intervals
area = 0
for i = 1 to n
x = a + i * deltaX
area = area + deltaX * f( x )
end of for
return areaThe algorithm above can be extended to evaluate higher dimensional integrals. For example, to evaluate
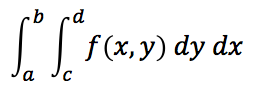
over the rectangular region a≤x≤b and c≤y≤d, you could use an algorithm that looks like this:
integrate2( f, a, b, c, d, n )
deltaX = ( b - a ) / n
deltaY = ( d - c ) / n
volume = 0
for i = 1 to n
x = a + i * deltaX
for j = 1 to n
y = c + j * deltaY
volume = volume + deltaX * deltaY * f( x, y )
end of for j
end of for i
return volumeThe algorithm can be extended in a similar way to handle integrals over 3 dimensions, 4, 5, and in general m dimensions.
Part B. How does the running time of this family of integration algorithms grow with n and m, the number of dimensions? You don’t have to write the general m-dimensional algorithm (and in fact can’t, with what we know so far about algorithms), and so don’t necessarily have to have a tidy derivation for your running time expression, but you should be able to explain sound reasoning for it in a combination of English and math.
Based on your answer to Part B, do you think people actually use Riemann sums to evaluate high-dimensional definite integrals? Why or why not?
Exercise 2.2-2 in our textbook (a loop invariant and execution time analysis for Selection Sort).
Exercise 3.1-1 in our textbook (prove that max( f(n), g(n) ) is in Θ( f(n) + g(n) )).
I will grade this exercise in a face-to-face meeting with you. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Please bring a written solution to the exercise to your meeting, as that will speed the process along.
Sign up for a meeting via Google calendar. If you worked in a group on this exercise, the whole group should schedule a single meeting with me. Please make the meeting 15 minutes long, and schedule it to finish before the end of the “Grade By” date above.