The William Lowell Putnam Mathematical Competition
1. Problem A1 – December, 2000
Let A be a positive real number. What are the possible values of 
, given that 
are positive numbers
for which 
2. Problem A1 December 1999
Find
polynomials f(x), g(x), and h(x), if they exist, such that, for all x,
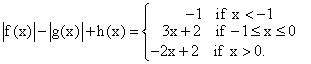
3. Problem A1
December 1975
Supposing
that an integer n is the sum of two triangular numbers,
write
4n+1 as the sum of two squares, 
, and show how x and y can be expressed in terms of a and b.
Show that, conversely, if , then n is the sum of two triangular numbers.
[Of course a, b, x, and y are understood
to be integers.]
4.
Problem B1 December 1975
In the additive group of ordered pairs of
integers (m,n) [with addition defined componentwise: (m,n) + (m’,n’) = (m +
m’,n + n’)] consider the subgroup H generated by the three elements
(3,8) (4,-1)
(5,4).
Then H has another set of generators of the form (1,b) and (0,a) for some integers a and b with a positive. Find a.
[Elements u and v generate H if every element h
of H can be written as mu + nv for some integers m and n.]
5. Problem A1 –
December 1973
Let there be given nine lattice points
(points with integral coordinates) in three dimensional Euclidean space. Show that there is a lattice point on the interior
of one of the line segments joining two of these points.
6. Problem A1 – December 1966
Let f(n) be the sum of the first n terms
of the sequence 0, 1, 1, 2, 2, 3, 3, 4,
4, 5,…, where the nth term is given by
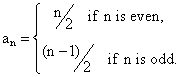
Show
that if x and y are positive integers and 
then 
7.
Problem
B1 December 1966
Prove that among any ten consecutive
integers at least one is relatively prime to the others.
8. Problem A1 December 1998
A
right circular cone has base radius 1 and height 3. A cube is inscribed in the cone so that one
face of the cube is contained in the base of the cone. What is the side length of the cube?
9. Problem A1 December 1974
Call a set of positive integers “conspiratorial” if no three of them are pairwise relatively prime. (A set of integers is “pairwise relatively prime” if no pair of them has a common divisor greater than 1.) What is the largest number of elements in any “conspiratorial” subset of the integers 1 through 16?
10. Problem A1 – December 1965
Let ABC be a triangle with angle A <
Angle C < 90° < angle B. Consider the bisectors of the external angles
at A and B, each measured from the vertex to the opposite side (extended).
Suppose both these line segments are equal to AB. Compute the angle A.
About the Putnam Competition
Archive of Past Problems and Solutions