Related Rates

Return to Course Outline

Previous Lecture

Misc

I’m Not Here Thursday

Canvas has a video chat feature (Blackboard Collaborate) that I want to try as a way of meeting class remotely.

Try connecting to Blackboard Collaborate to be sure you can and to see if having all of us on it overloads anything.

• I recommend not turning microphones on for more than 1 computer in the same room, to avoid feedback.
• For future reference, there’s a video demonstration of how to connect to Blackboard Collaborate.

For a recording of the session as it actually happened, click here.

Questions?

Exam Problems?

Question 5 (based on a graph, where is the derivative greatest): the derivative is greatest where the slope of the graph looks greatest, i.e., around x = 0, because the derivative represents the rate of change or slope.

Question 4 (the rate at which apparent height is changing): the numeric answer is 0.001 feet/second, but note that most of what I’m looking for in grading it is that you know what the relevant derivative is and how to set up its calculation, not whether you get 0.001.

Related Rates Problems

Section 4.1

Example. There’s an old farm silo on my property. For a few weeks each fall the sun rises at just the right time for me to look out the window during breakfast and see the silo casting a long shadow across the fields. If the silo is 30 feet tall, how fast is the shadow shrinking when the sun is 5 degrees above the horizon?

Reading ideas: This problem involves a rate because something changes

• In fact it involves related rates, because it’s asking for an unknown rate (the rate at which the shadow contracts) that is related to a known, or at least knowable, one (the rate at which the angle to the sun changes).
• A process for solving related rates problems:
  1. Find an equation that relates the given quantities.
  2. Find an equation relating rates by differentiating the first equation via the chain rule.
  3. Substitute known values into the equation for the derivatives.
  4. Solve for the unknown derivative.

The tangent function seems relevant to this problem.

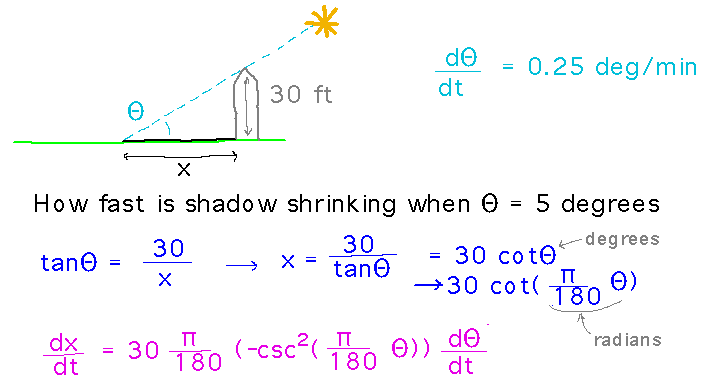
Plugging the values of Θ (5 degrees) and dΘ/dt (0.25 degree/minute) into the formula for dx/dt, and evaluating it in Excel, we found that the shadow is shrinking at roughly 17 1/4 feet per minute.

Notice that we needed to differentiate a trigonometric function whose argument was in degrees here. That’s not the same as differentiating when the angle is in radians, because the derivations of the trigonometric derivatives ultimately trace back to the relationship between angles in radians and a circle’s radius. But converting degrees into radians isn’t hard, for example as with sine:

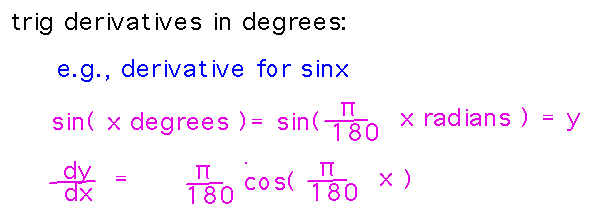
Example. Imagine a drone with a camera that points straight down. The camera has a 30 degree field of view. The drone is rising at a speed of 10 feet per minute. How fast is the area seen by the camera increasing when the drone is 100 feet high?

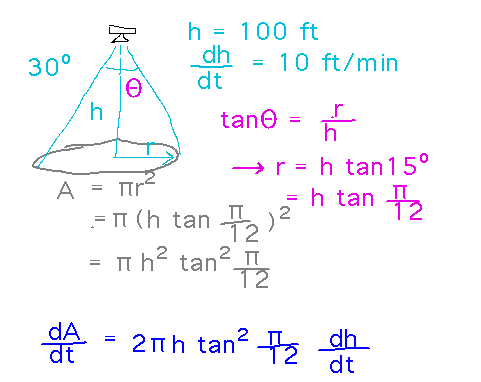
Numerically, dA/dt = 451 sq ft/min

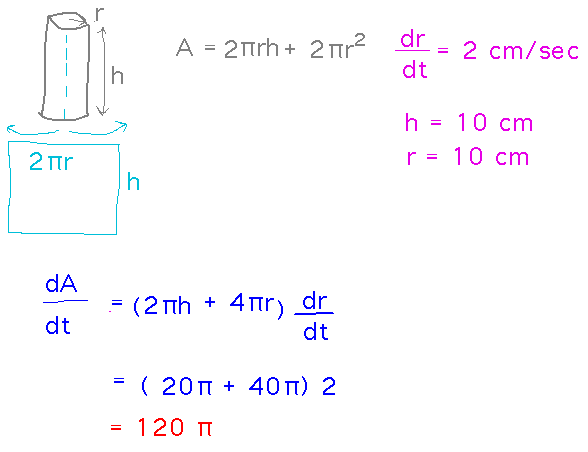
Example. Suppose a cylinder 10 cm long is inflating in such a manner that its radius increases by 2 cm/sec. How fast is its surface area (including the ends) increasing when the radius is 10 cm?

Example (what I think of as the totally stereotypical related-rates problem). A 20 foot ladder is sliding down a wall at a rate of 1 foot/second. How fast is the bottom of the ladder sliding away from the wall when the top of the ladder is 10 feet above the ground?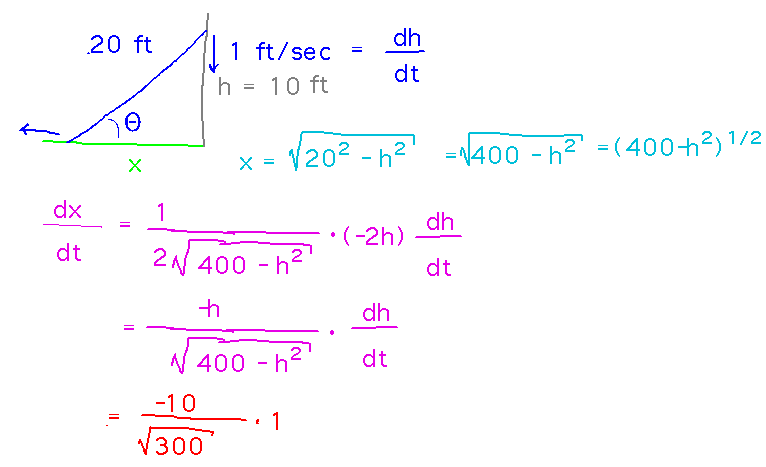

Take-Aways. The most important lesson from all these examples is the practice they provide with concretely carrying out the related rates process outlined at the beginning of these notes.

Also notice how often it was helpful to have diagrams of the objects or situation in the problems.

Next

Linearization and differentials.

Read section 4.2

Next Lecture