Misc
Colloquium
“History of Calculus”
By Professors Jeff Johannes and Gary Towsley
Wednesday, November 15, 2:30 PM
Newton 204 (get there a bit early to be assured of a seat)
Extra credit for writing a paragraph about connections you make to the talk, as usual.
Questions?
For problem 1 on problem set 9, you just need to find the derivative.
Definite Integral Applications
Area
Find the area between the x axis, the graph of y = x3, and the lines x = 0 and x = 2.
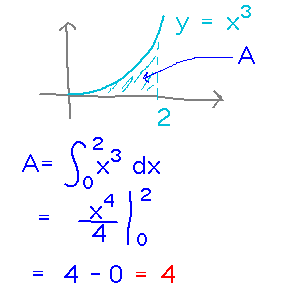
How about the area between the axis, x3, and x = -1 to x = 2?
This exposes the fact that integrals, unlike geometric areas, are signed. If you really want area “under” a curve and that curve is negative sometimes, you need to break it up into regions where it’s positive and ones where it’s negative, and subtract the negative “areas” from the positive ones.
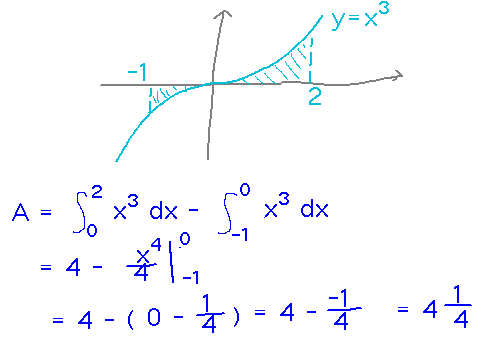
Net Change
If I drop or throw a ball with initial upward speed v, its upward speed t seconds later is v - 32t feet per second.
So if I drop a ball from height 0 with initial speed 0, what is its height 2 seconds later?
If I throw the ball up with initial speed 64 ft/sec, what is its height after 1 second? How about after 3 seconds?
Reading ideas?
This is based on the net change theorem, i.e., that the final value of a function F with derivative f is the initial value F0 plus the integral of f over whatever range you want a “final” value at the end of.
The upward moving ball with the same height after 1 and 3 seconds demonstrates why this is net change: the ball certainly kept moving between 1 and 3 seconds, and so moved farther than 48 feet total, but by the end of the 3 seconds it had stopped rising and fallen back to where it was after 1 second, for the same net change in position.
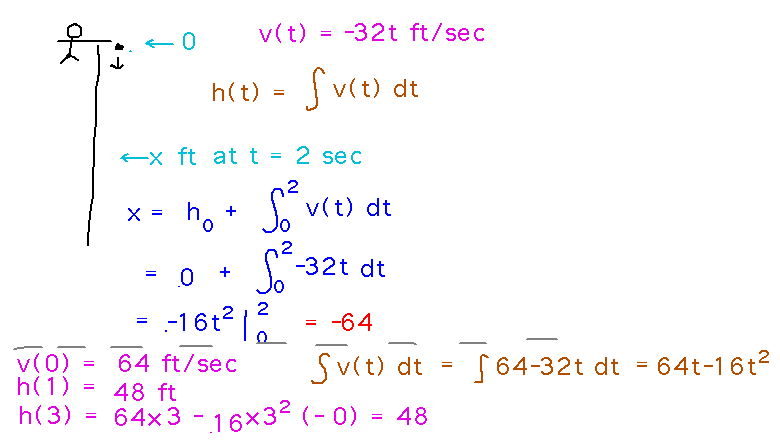
Next
Substitution: an “antiderivative” tactic for the chain rule.
Read section 5.5.