SUNY Geneseo Department of Mathematics

Area Between Curves

Monday, November 20

Math 221 05
Fall 2017
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Colloquium

Jamie Juul, Amherst College (faculty candidate).

Today (November 20), 4:00 PM, Newton 201.

“The Birthday Problem and a Problem in Arithmetic Dynamics”

Extra credit for writing a paragraph about connections you make to it, as usual.

Questions?

Area Between Curves

Section 6.1

The Basic Idea

Find the area between the graphs of y = x2 + 1 and y = -x2, between the lines x = -1 and x = 1.

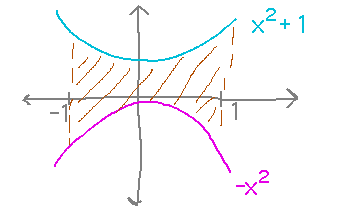
Upward and downward parabolas with the area between shaded

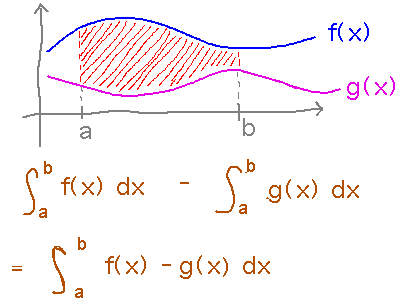
Reading ideas: Subtract the area below the lower curve from the area below the upper one.

Curves f(x) and g(x) with area in between shaded; that area is integral from a to b of f minus integral from a to b of g, or the integral from a to b of f(x) - g(x)

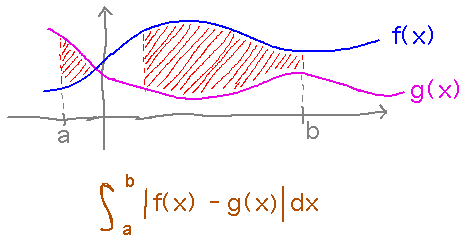
But the book also includes an absolute value in the integral, which handles the possibility that the curves cross. This matters, but means that it’s no longer quite right to say that this is just the difference of two integrals.

Curves f(x) and g(x) cross; area is integral from a to b of abs( f(x) - g(x) )

Apply this idea to x2+1 and -x2:

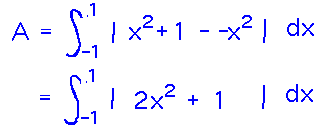
A = integral from -1 to 1 of abs( x^2 + 1 - -x^2 ) which is the integral from -1 to 1 of abs( 2x^2 + 1 )

Now the function in the integrand is always positive, so we can remove the absolute value and find an antiderivative:

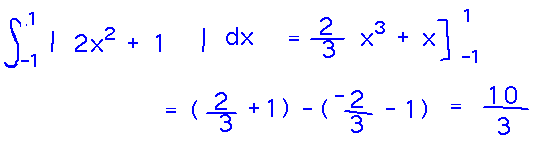
Integral from -1 to 1 of abs( 2x^2 + 1 ) is 2/3 x^3 + x evaluated from -1 to 1, or 10/3

Curves that Cross

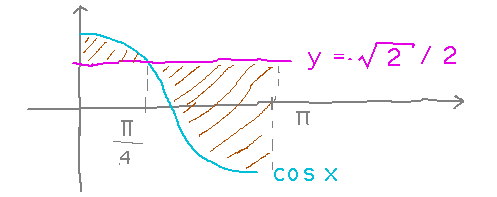
Find the area between the line y = √2/2 and the graph of y = cos x over the interval 0 ≤ x ≤ π.

Flat line across a cosine curve with shaded areas above and below line to cosine curve

Set up the integral the same way as before:

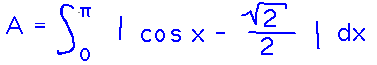
A = integral from 0 to pi of abs( cosx - sqrt(2)/2 )

But this time the curves intersect at π/4, so the absolute value matters — it flips the sign of the integrand at x = π/4. Handle this by splitting the integral and negating the integrand in the second part:

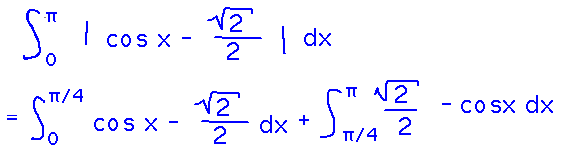
integral from 0 to pi of abs( cosx - sqrt(2)/2 ) = integral from 0 to pi/4 of cosx - sqrt(2)/2 plus integral from pi/4 to pi of sqrt(2)/2 - cosx

And now the individual integrals can be evaluated in the usual way:

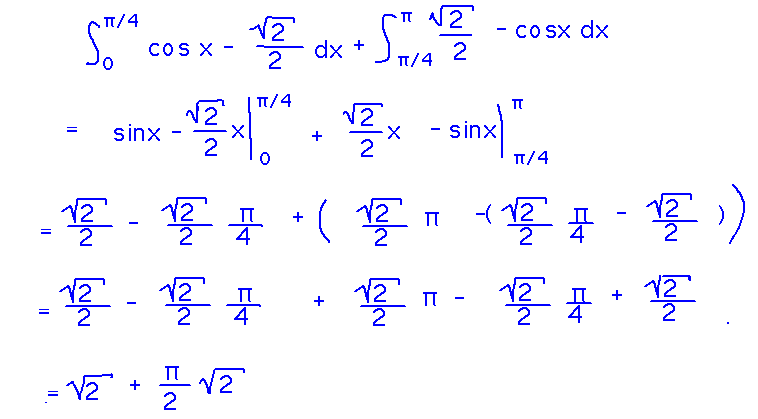
Integral from 0 to pi/4 of cosx - sqrt(2)/2 plus integral from pi/4 to pi of sqrt(2)/2 - cosx = sinx - sqrt(2)/2x evaluated from 0 to pi/4 plus sqrt(2)/2 - sinx evaluated from pi/4 to pi which equals sqrt(2) + pi sqrt(2)

Take-Aways

The central idea in finding the area between curves is to integrate the difference of the relevant functions.

But beware that this difference must always be positive in order to get the correct positive area; formally this is described by integrating the absolute value of the difference, and practically by splitting the integral at points where the functions’ curves cross.

Next

Calculating volumes.

Read section 6.2 through “The Disk Method.”

Next Lecture