Volume by Shells: Examples

Return to Course Outline

Previous Lecture

Misc

Problem Set 11

Change part 2 of problem 5 to be “when the depth of the water is 1 inch” (rather than “when the volume is 100 cubic inches”).

Final

Thursday, December 14, 8:00 AM, in our MWF Sturges classroom.

The exam will cover the whole semester, but emphasizing material since the second hour exam (e.g., the Fundamental Theorem; substitution; area, volume, and similar applications of definite integrals; etc.)

Roughly 2 to 2 1/2 times as long as the hour exams in terms of number of questions and design time. But note that you have roughly 4 times as long in terms of actual time, so there should be less time pressure.

The rules and format will otherwise be the same as on the hour exams, particularly the open-references and calculator rules.

I’ll bring donuts and cider.

SOFIs

Available from now through December 12.

Please fill them out — they’re useful to me in improving courses over time, especially written comments.

Get to the SOFI survey via Knightweb.

Questions?

Volume by Shells

Core Idea

Find the volume enclosed by a parabolic lampshade whose profile is the curve y = 4 - x² for x ranging from 0 to 2.

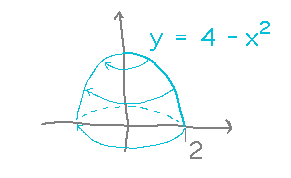
To set this up via shells, imagine a thin-walled cylinder inside the lampshade, and think about the volume of that cylinder’s wall:

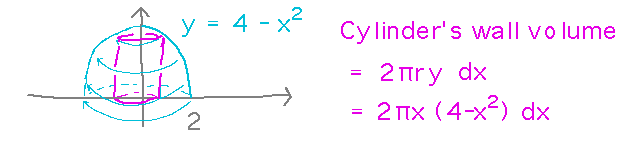
Now the volume of the lampshade is the (Riemann) sum of the volumes of all the cylinder walls, i.e., the integral of the volumes of infinitely thin cylinder walls:

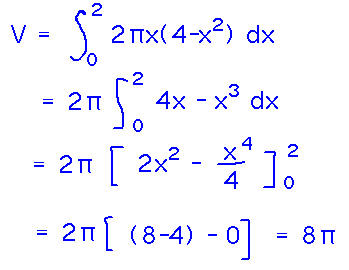
A More Complicated Example

Consider a cone whose wall’s cross section is the region between the lines y = 2x and y = x for x ranging from 0 to 2. What is the volume of the wall?

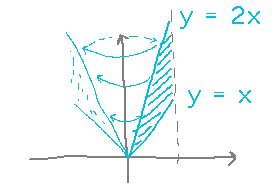
Once again, start by imagining the cone wall divided into thin cylinders. But this time the height of the cylinders isn’t just one of the functions involved (2x or x), it’s their difference:

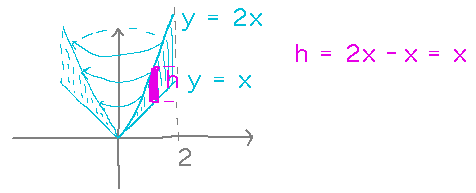
The basic integration is the same as before, integrating the volumes of all the cylindrical shells:

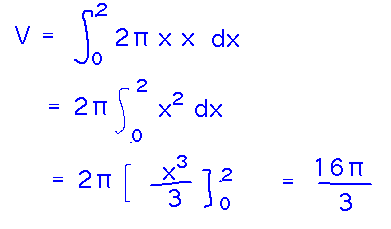
Shells or Disks?

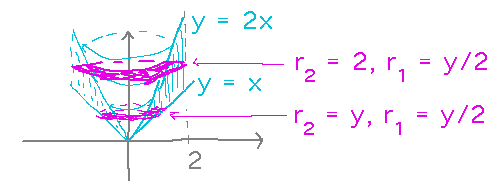
You can generally find volumes of revolution using either the shell method or the disk/washer method. Sometimes though one is easier to set up than the other. For example, if we tried to do the above cone by washers, we’d find that the expression for the outer radius changes part way through, and so we have to evaluate 2 integrals:

Take-Aways

To find a volume of revolution via cylindrical shells...

1. Figure out how to divide the volume into shells, and particularly how the height (h) of each shell depends on distance (r) from the axis of revolution.
2. Integrate 2πrh over the appropriate range of whatever variable determines r and h.

You can generally find volumes of revolution using either the shell or the disk/washer methods, but depending on the problem, one method might be easier to set up and evaluate than the other.

Next

Finding lengths via integration.

Read sections “Arc Length of the Curve y = f(x)” and “Arc Length of the Curve x = g(y)” in section 6.4 of the textbook.

Next Lecture