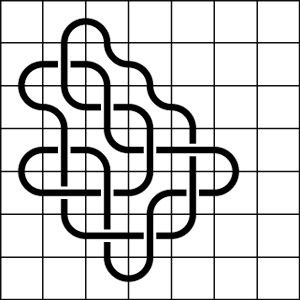
Knot Mosaics for the 1021 Knot
For many knots, the tile number and/or crossing number cannot be realized when the mosaic number is realized.
The mosaic of the 1021 knot given in the table has the mosaic number realized, which is 6, but the tile number and crossing number of this knot cannot be realized on a 6-mosaic. On a 6-mosaic, the fewest number of non-blank tiles needed to create this knot is 32. However, the tile number of this knot is 27, and this cannot be realized on anything smaller than a 7-mosaic. The crossing number is also first realized on a 7-mosaic, but at least 29 non-blank tiles are necessary to achieve it. Below are the relevant mosaics.