A Preview of Calculus

Return to Course Outline

Previous Lecture

Misc

Math Learning Center

Excellent tutoring resource for this and similar courses.

In South 332.

Opens for the semester Wednesday, Sept. 6, at 10:30 AM.

Open house Wednesday, 2:30 - 3:20 PM.

Problems Opening Matlab?

Mac users often have trouble with an “application from unknown developer” error message when trying to launch Matlab for the first time -- see the instructions for installing it for a solution.

If all else fails, ask the CIT helpdesk.

Questions?

Preview of Calculus

Section 2.1

Derivatives

Problem. Find the slope of the secant line to the function f(x) = 2x² between x = 1 and x = 2.

Find the equation for this line.

These questions draw on the book’s definition of a secant line as the line between 2 points on a curve, and its formula for the slope of a secant line (but note that the order of the points in that formula isn’t as important as it sounds in the book, as long as you are consistent about the order of the “x” and “a” terms in the numerator and denominator).

The equation for the line comes nicely from the point-slope equation for a line, y = m(x-x₁) + y₁, where m is the slope and (x₁,y₁,) is the point (not in this section).

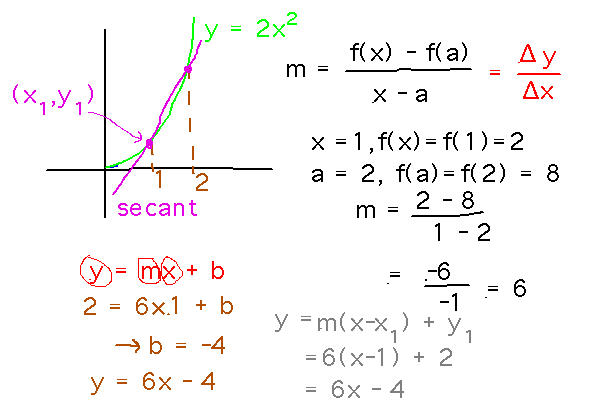
Problem. Estimate the slope of the tangent line to f(x) = 2x² at x = 1.

This involves repeated use of the secant slope, for secant lines between points ever closer to (1,2).

A spreadsheet is a really good, if under-appreciated, tool for doing this sort of repetitious calculating. Here’s one for this problem, suggesting that the slope of the tangent is 4 or at least very close to 4.

Summary. Geometrically, the derivative of f(x) at x = a is the slope of the tangent to f at x = a; this tangent can be approximated by a line between (a,f(a)) and (x,f(x)) for some x very close to a. This idea is the starting point for defining the derivative, and the above problems illustrate it.

Definite Integrals

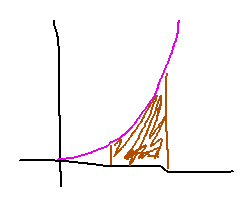
Summary. Geometrically, the definite integral of a function is the total area below the curve but above the x axis. Estimating the area by a sum of very narrow rectangles is the key idea behind the definition of the definite integral.

Connections

Surprising fact: these ideas are opposites (in formal mathematical terms, “inverses”) of each other -- If function F describes the area under the curve of function f, then f also describes the slope of F.

Do you see any other common theme to derivatives and definite integrals?

• Both involve figuring out something’s limit behavior. So the first thing to understand in order to do calculus rigorously is limits.

Problem Set

Handout

Next

Limits

Read the introduction and “Intuitive Definition of a Limit” subsections of section 2.2

Next Lecture