Questions?
Derivatives at a Point
Section 3.1
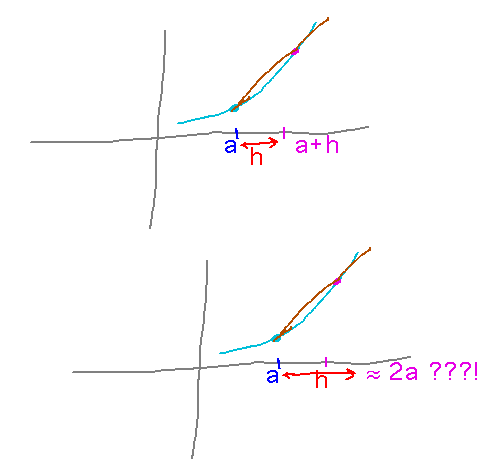
Typo. Practically the first paragraph about tangent lines has a typo regarding h. What is it and what should the text say?
The value of h needn’t be close to a. Rather, the idea is that h is small, i.e., close to 0.
Example. Find the derivative of f(x) = 7x - 3 at x = 2. In other words, what is f′(2)?
Reading ideas: Use the formula for f′(a), either the version in terms of x approaching a or the version in terms of h approaching 0.
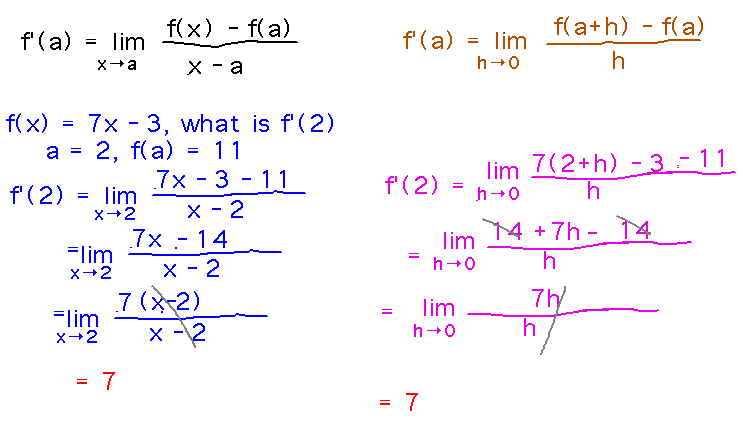
Could you also keep a as the variable and work out a general f′(a) = 7?
Yes, and in fact that’s how you get derivatives as functions, not just as things to calculate in isolation for individual points.
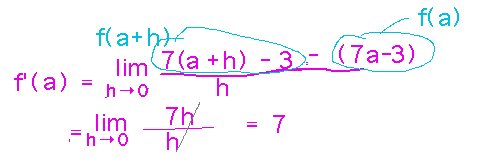
Example. Suppose you’re moving in such a way that your speed at time t is given by s(t) = 3√t feet per second. How fast is your speed changing when t = 1?
Reading ideas: derivatives are rates of change, so the answer to this question is s′(1).
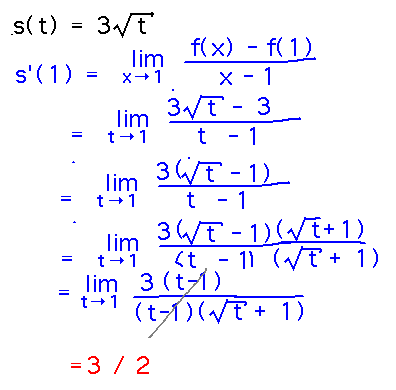
Take-Aways. The most important thing in this section is the definition of the derivative at a point as a limit (or more accurately, either of two equivalent limits).
The idea that a derivative is a rate of change is the source of a lot of the real-world importance of derivatives.
Problem Set
See handout.
Next
The derivative as a function.
Read section 3.2