SUNY Geneseo Department of Mathematics

The Mean Value Theorem

Wednesday, October 18 - Thursday, October 19

Math 221 05
Fall 2017
Prof. Doug Baldwin

Misc

Exam 2

So far, people who’ve had an opinion would like to move exam 2 to Thursday, November 2.

Particularly if you don’t want this change, let me know before tomorrow’s class -- otherwise I’ll make it official in class.

Colloquium

“The Mathematics behind Emerging Data Science and Machine Learning”

Yusuf Bilgic, SUNY Geneseo

Thursday, October 19, 4:00 PM, Newton 203.

Extra credit for paragraphs about how you connect to it. “Due” before final exam.

Questions?

The Mean Value Theorem

Section 4.4

Examples

Secant Lines. Think back to the first few days of this course and calculations of slopes of secant lines.

For example, consider f(x) = x² between x = 0 and x = -1. What’s the slope of the secant line?

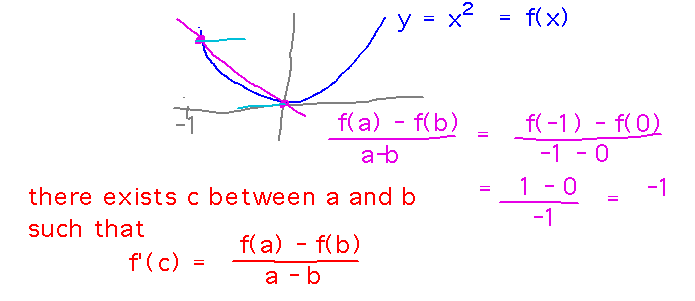
f(x) = x^2, a = -1, b = 0, then (f(b)-f(a))/(b-a) = -1

What do you learn about the derivative from the slope of the secant line?

“On average” the derivative is -1 (for an imprecise notion of “average”).
But more importantly, there is some x value between -1 and 0 where f′(x) is exactly -1.

What does this have to do with the reading?

The Mean Value Theorem says that somewhere between x=a and x=b, the derivative of f is equal to the slope of the secant line between (a,f(a)) and (b,f(b)).
But only if f is continuous and differentiable between a and b.

Example. If I push a ball off a 1-meter-high table, its height from the floor after t seconds is 1 - 5t² meters. How long does it take to reach the floor?

What is its average speed?

Is its instantaneous speed ever equal to that average? Who says? If so, when?

Find time by solving h = 0 for t; average speed = change in h over change in time; solve dh/dt = average to find c.

The Mean Value Theorem says that the instantaneous speed must at some time equal the average, and the c we found is the time when that happens. It’s consistent with the intuition that the average speed occurs at half of the total time.

Antiderivatives. We know that functions of the form F(x) = x³ + x² + C are antiderivatives of f(x) = 3x² + 2x. Are there any other antiderivatives of f? Why or why not?

Hypothesis (“Dina’s Theorem”): there are no other antiderivatives because if there were, they would have to have different shapes from each other, which implies different slopes and thus different derivatives, but there’s only one derivative here.

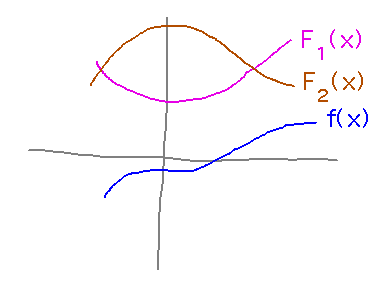
One derivative curve but two alleged antiderivatives with different slopes

The textbook proves a special case of this, namely if the derivative is always 0 then all antiderivatives are constants.

From that, the book proves the “constant difference theorem”: if f′(x) = g′(x), then f(x) = g(x) + C. This theorem assures that we know how to find all the antiderivatives of a derivative (as long as we know how to find one at all); we know more about antiderivatives than you might have thought.

Rolle’s Theorem

What does Rolle’s theorem say, and what does the book prove?

Rolle’s theorem: if f(a) = f(b), then somewhere between x=a and x=b, f′(x) = 0 (for a continuous and differentiable function f).

But part of the book’s proof assumes more, namely that f(a) = f(b), and in addition that what they equal is 0. This isn’t right for the theorem as stated, and should be f(a) = f(b) = k. The argument given for f(a) = f(b) = 0 can be adapted to the more general (and correct) case f(a) = f(b) = k.

Inferring the shapes of curves from their derivatives.

Read section 4.5.

Next Lecture