Horizontal and Oblique Asymptotes

Questions?

Asymptotes

Section 4.6

Horizontal

Concept. Sketch some functions that have horizontal asymptotes.

Reading ideas: horizontal asymptotes occur when a function has a constant limit as x approaches positive or negative ∞. Note that simply having a place where the graph of the function becomes horizontal isn’t enough, it has to stay or become ever more horizontal as x gets further from 0.

Inverse tangent (technically you don’t need to know there is such a thing until calculus 2, but most of you have probably seen it as arctan):

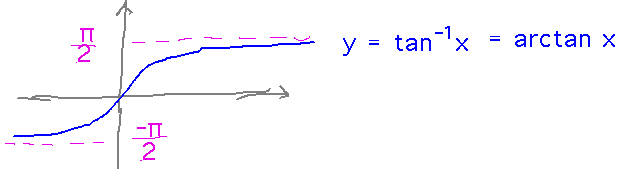
(2x²-3x) / (x²+1) from last class, which we know has a horizontal asymptote because we found one by taking the limit as x approaches ∞. And in fact it only has one horizontal asymptote, because the limit calculation would proceed in essentially the same way if x were approaching -∞.

These examples show that functions can have either one or two values they approach as horizontal asymptotes.

Examples. Find the horizontal asymptotes, if any, of f(x) = 2 / (x²-1).

Find the horizontal asymptotes, if any, of y = 3x / (x+3).

Find the horizontal asymptotes, if any, of g(z) = (z² - 2) / (z+1).

Reading idea: finding a constant limit as x (or z in example 3) approaches positive or negative ∞ shows that a function has a horizontal asymptote. The limit is the asymptote.

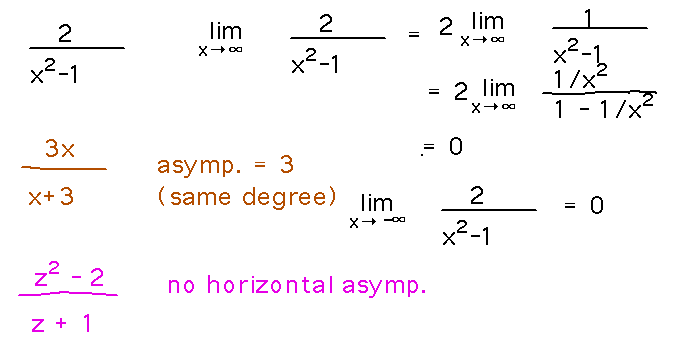
Oblique Asymptotes

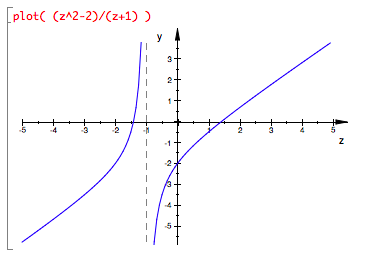
What can you say about asymptotes of (z² - 2) / (z+1)?

• It doesn’t have horizontal ones.
• It does have a vertical one at x = -1.
• It does have an oblique one, i.e., as z approaches positive or negative ∞ the function becomes more and more linear. Here’s what that looks like graphed by muPad:

Take-Aways

Horizontal asymptotes exist wherever a function approaches a constant as its argument becomes infinitely large or small.

Find horizontal asymptotes by finding the limit the function approaches, if any. Shortcuts exist for doing this for rational functions.

Oblique asymptotes can also exist, notably in rational functions whose numerators have degree one higher than the degree of the denominator.

Next

Optimization problems.

Read section 4.7.