Limits at Infinity

Return to Course Outline

Previous Lecture

Misc

Course Comments

Please return questionnaires by Friday (Oct. 27), if you want to return them.

Problem Set 7

Mostly covers extreme values, shapes of graphs, etc.

See handout for details.

Questions?

Limits and Asymptotes

Section 4.6

The Foundation

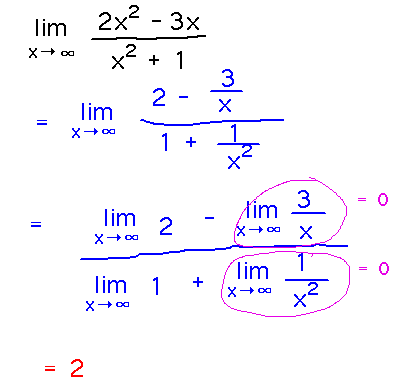
Examples. Find lim_x→∞ (2x² - 3x)/(x²+1)

Describe the end behavior of f(x) = x sinx

Does y = (3x + 2)/5x have any horizontal asymptotes? If so, where? What about oblique asymptotes?

Commonalities. What common idea from the reading underlies solving all of these problems (and similar ones)?

• Limits as x becomes infinite
• So understanding those limits is the starting place for understanding the whole section.

Theory and Application

Like many other kinds of limits, working with limits as x approaches ∞ is best done by identifying a few relevant laws and then trying to use algebra or other laws to rewrite specific limit problems into forms to which those laws apply.

One major law is that lim_x→∞ (1/x^k) = 0. Prove it.

Reading idea: lim_x→∞ (f(x)) = L if for all ε, there exists an N such that if x > N, then |f(x)-L| < ε

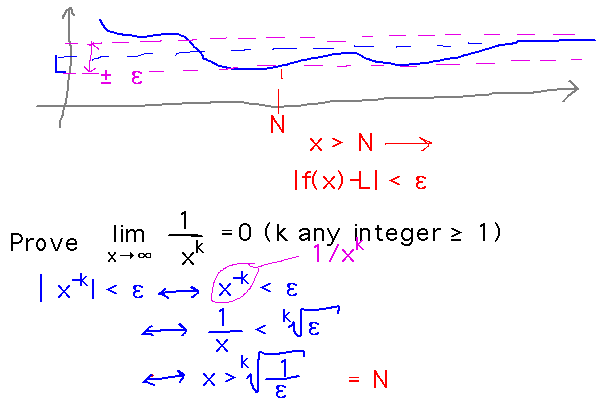
Finding limits. Find lim_x→∞ (2x² - 3x) / (x² + 1)

Reading idea: When the numerator and denominator of a ratio of polynomials have the same degree, the limit is just the ratio of the coefficients of the highest-degree term. So in this case the limit should be 2.

Verify this by rewriting the limit and using limit laws.

Take-Aways

Two important laws regarding limits as x approaches ∞

• lim_{x → ∞} x^k = ∞
• lim_{x → ∞} 1/(x^k) = 0

Dividing by the highest power in the denominator is generally a good trick for finding limits of rational functions (ratios of polynomials).

Next

Asymptotes.

Finish reading or review section 4.6.

Next Lecture