Injections, Surjections, and Bijections

Return to Course Outline

Previous Lecture

Misc

GREAT Day is next Wednesday (April 17).

Lots of math talks and posters; go see them (and other things, too).

Extra credit for writing reactions/reflection on any one math-related presentation.

Questions?

Injections, Surjections, Bijections

Section 6.3.

Definitions

Sketch arrow diagrams for stereotypical injection, surjection, bijection, and for examples of key disqualifying features.

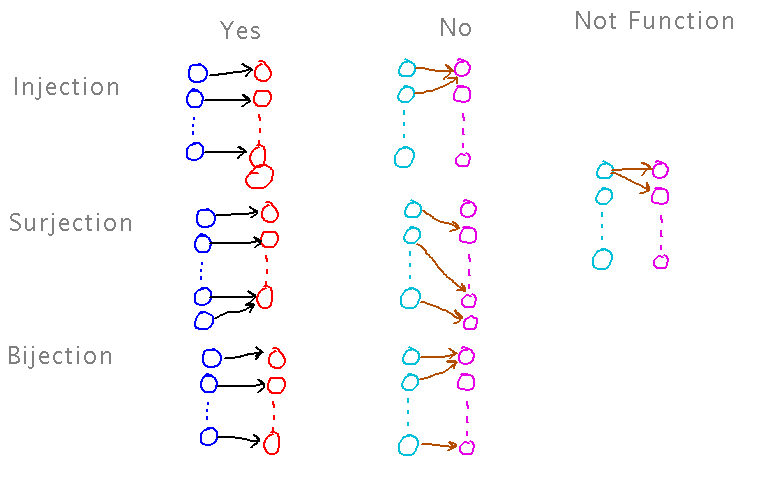
Proofs

Consider f : ℕ → D, where D is the set of odd natural numbers, defined by f(n) = 2n - 1.

Prove that f is an injection, surjection, and bijection.

Formal versions of these proofs are here, with LaTeX source here. The following are outlines of the proof ideas.

Injection

Proof 1, by contradiction: assume a ≠ b but f(a) = f(b), so

2a -1 = 2b - 1

2a = 2b

a = b

...which is a contradiction because a ≠ b.

Proof 2, via the contrapositive: assume f(a) = f(b), show a = b

2a -1 = 2b - 1

2a = 2b

a = b

QED.

Notice that this uses the same algebra as the contradiction proof, but in a slightly more direct way.

Surjection

Let y be in D, and show there’s an n such that y = f(n) = 2n - 1. If y = 2n - 1 then...

2n = y + 1

n = (y+1)/2

Check: f((y+1)/2) = 2(y+1)/2 - 1 = y+1 - 1 = y.

Bijection

Immediate because f is an injection and a surjection.

Key Points

Definitions of injection, surjection, and bijection.

Prove that a function is an injection by showing that f(a) = f(b) implies a = b

Prove that a function is a surjection by showing that a generic element of its codomain has a preimage. This is essentially choose-an-element.

Prove that a function is a bijection by proving it is an injection and a surjection.

Composition

The composition of functions f and g is f(g(x)), often written f ∘ g.

Not too suprisingly, if f and g are injections, surjections, and/or bijections, so is f ∘ g. (These are all theorems that can be proven.)

Next

Inverses of functions.

Read section 6.5

Next Lecture