|
|
|
|
|
My name is Aaron Heap, and I live in Geneseo, New York. I was born and raised in Frederick, Oklahoma. I then moved to Fort Worth, Texas, where I attended college at Texas Christian University. I graduated from TCU with a bachelor's degree in mathematics. After college I moved to Houston, Texas, where I attended graduate school at Rice University. I graduated from Rice in 2004 with a Ph.D. in mathematics. I lived in Rochester, NY, for 3 years where I worked as a visiting professor in the Department of Mathematics at the University of Rochester.
Currently I am a professor in the Department of Mathematics at the State University of New York at Geneseo, and I have been here since 2007.
I was married to my wonderful wife, Bridgette, in June 2007. She is an exceptional woman, and we are enjoying life together. Our daughter Clarissa was born in June 2012, and our son Dalton was born in June 2014. We also have a wonderful dog named Rhubarb.
"Life is good for only two things, discovering mathematics and teaching mathematics." --Siméon Poisson
"To raise new questions, new possibilities, to regard old problems from a new angle requires a creative imagination and marks the real advances in science. The important thing is to not stop questioning." --Albert Einstein
I am a math professor at the SUNY Geneseo. My field of study is algebraic topology. More specifically, I study classical 3-dimensional manifold topology, mapping class groups, bordism theory, and knot theory. I wrote my dissertation, "Bordism Invariants of the Mapping Class Group", under the direction of my advisor Tim Cochran. The picture to the right is of Tim with his most recent students at the time of my graduation: myself (2004), Connie Leidy (2004), Shelly Harvey (2002), Carol Gwosdz Gee (2004), Steve Wallace (Masters, 2004), Amy Lampazzi (2001).
The field of algebraic topology is an area of mathematics in which one uses algebraic techniques to study topological shapes and spaces. A typical process is to associate an algebraic group with a topological space in such a way that homeomorphic spaces are assigned isomorphic groups. In other words, if the spaces "look the same" then their associated groups should also "look the same." Such algebraic groups are called topological invariants.
In my research I am investigating the mapping class group of 2-dimensional spaces called manifolds or surfaces. The mapping class group is the set of homeomorphisms, or self-equivalences, of these surfaces. An example of such a homeomorphism is pictured here.
Example of an element of the mapping class group
Each element of the mapping class group may also be associated to 3-dimensional manifolds.
In particular, given a 3-dimensional manifold, one can construct another by cutting it open along an embedded surface and regluing it in a different way. Essentially, the mapping class group is the set of different ways to do this regluing. Given two 3-dimensional manifolds, we say that they are bordant if together they form the boundary of a 4-dimensional manifold. The 4-manifold is called a bordism. In this picture to the right, we see an example of a 2-dimensional bordism between 1-dimensional manifolds. Similarly one can easily see that the boundary of 3-dimensional objects is 2-dimensional. Can you picture a 4-dimensional bordism between 3-dimensional spaces??? This may seem unimaginable merely because we can't really visualize 4-dimensional objects, but the idea is completely analogous and is just the next step up from these examples. My results determine which elements of the mapping class group allow the resulting 3-dimensional manifold of the regluing mentioned above to be bordant to the original 3-dimensional manifold.
Knot theory is the study of knotted and linked simple closed curves in
3-dimensional space (or in general, knotted and linked n-dimensional spheres in (n+2)-dimensional space.) Knot theory is one of the most active areas of mathematics today. Despite
being a field that is over a century old, some of the most exciting results have come in recent years.
The possibility of studying knots is thought to have been first recognized by Gauss in the 1830s, and the first attempts at classifying knot types were made about 50 years later. However, the theory truly blossomed with the development of topology and algebraic topology, which began around the turn of the century. The study of knots has led to important applications in DNA research and molecular biology. It also is making a significant impact on statistical mechanics and quantum field theory.
Knot theory is often considered popular simply from a visual standpoint (see the nice pictures here for example,) but the mathematics behind knot theory is also very elegant. Another great aspect of knot theory is its very broad range of difficulty. At one end of the spectrum, there are questions that can be understood and answered by little children, and high school students have proven their own theorems. At the other end of the spectrum, there are many mathematicians with PhD's who build their careers around questions in knot theory, and there are many questions that appear virtually impossible to answer.
Yggdrasil, the tree of Norse mythology whose branches lead to heaven, is realized here as Alexander's horned sphere. (Drawn by Bill Mayers, from Rolfsen's Knots and Links, 1976)
This is a view of knotted DNA as viewed through an electron microscope. (From Wasserman, Dungan, and Cozzarelli, 1985)
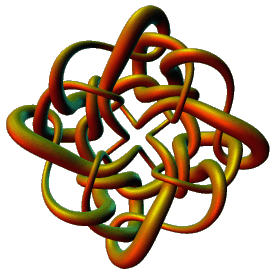
"Knots and Their Manifold Stories" math conference at the Banff International Research Station in Banff, Canada
"Topology of Manifolds of Dimensions 3 and 4" math conference celebrating Andrew Casson's 60th birthday
Quotations
I am a big fan of history and famous quotations. Here are a few famous and some not-so-famous ones for you to enjoy in my Page of Quotations for just a few of my favorite quotes.
Here are some quotes related to mathematics in my small collection of math quotes. Or you can see more at these sites:
Religion
The most important thing in my life is my Christian faith. The most important and most influential person in my life is my Lord and Savior, Jesus Christ. Despite the scoffers, mockers, and doubters that I encounter in my daily struggle, I try to do my best to keep the faith and stand strong. When it seems like the world is collapsing around me, my Lord gives me the strength I need to press on toward the goal which He has set for me. When it seems like all is hopeless, it is my faith that keeps me going.
One of the most rewarding experiences I've ever had was serving as the youth pastor for the First Christian Church of Houston, Texas. All of those kids are wonderful people and great friends. Some of them are pictured here to the right.
The 17th-century mathematician and philosopher Blaise Pascal concluded that faith is sometimes just a gamble. He told his friends, "If I believe in God and life after death and you do not, and if there is no God, we both lose when we die. However, if there is a God, you still lose and I gain everything."
"I have fought the good fight, I have finished the race, I have kept the faith." -- 2 Timothy 4:7
Return to my professional page.
