Geneseo Mathematics Colloquium

Geneseo Mathematics Colloquium
Spring 2024
Wednesday, March 27, 2024
3:30 pm
Newton 204
Mathematics and Science Fiction
Ruhan Zhao, SUNY Brockport
Abstract: In this talk we will discuss relations between Mathematics and Science Fiction. The topics include mathematicians who write Science Fiction and Mathematics in Science Fiction novels and stories.
Fall 2023
Friday, November 17, 2023
4-5 pm
Newton 203
The Cultural Context of Calculus and the Curious Complications of Convergence
Jeff Johannes
Abstract: Across the country and world, millions of people are studying calculus right now, just like you are. Why? Because it’s useful? Yes, that’s true. Because it’s interesting? We believe that’s true, even if you don’t as much. How about this … because it is one of the most important and significant accomplishments of humanity? In this talk I will explore this claim - to see what culturally led to the creation of calculus and the societal consequences of calculus. As a demonstration of the interconnectedness of the mathematics, I will explore the history of limits and how they ended up being the most recently developed material that you learn in introductory calculus. Come join us to see why calculus matters.
Friday, October 20, 2023
4:00 pm
Newton 214
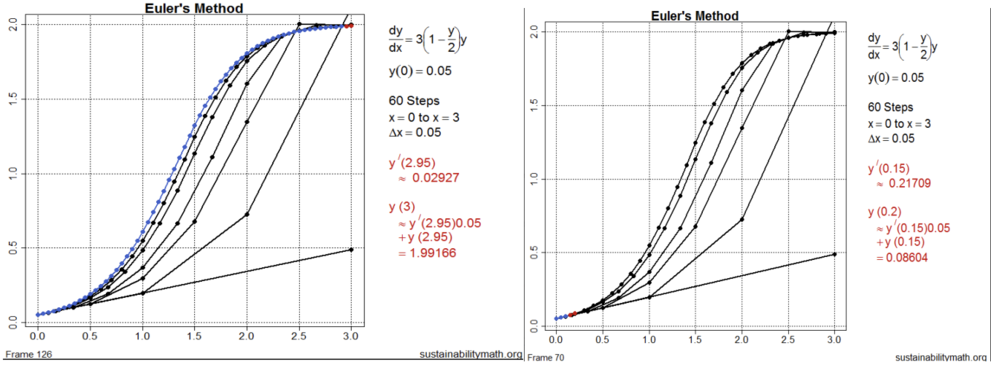
Mathematics in the Age of Computation
Thomas Pfaff, Ithaca College
Abstract: Mathematica, which is 35 years old, and the TI-89 calculator, which is 25 years old, are both impressive instruments with shortcomings. Mathematica is an expensive program that is not widely used in industry. The TI-89 calculator is cumbersome and unsuitable for significant computing. Meanwhile, R, and Python are powerful, free, and widely used programming languages. This talk will discuss how R may be used to improve mathematics, starting in calculus and focusing on modeling and Euler's method.
Thursday, September 21, 2023
2:30 pm
Newton 214
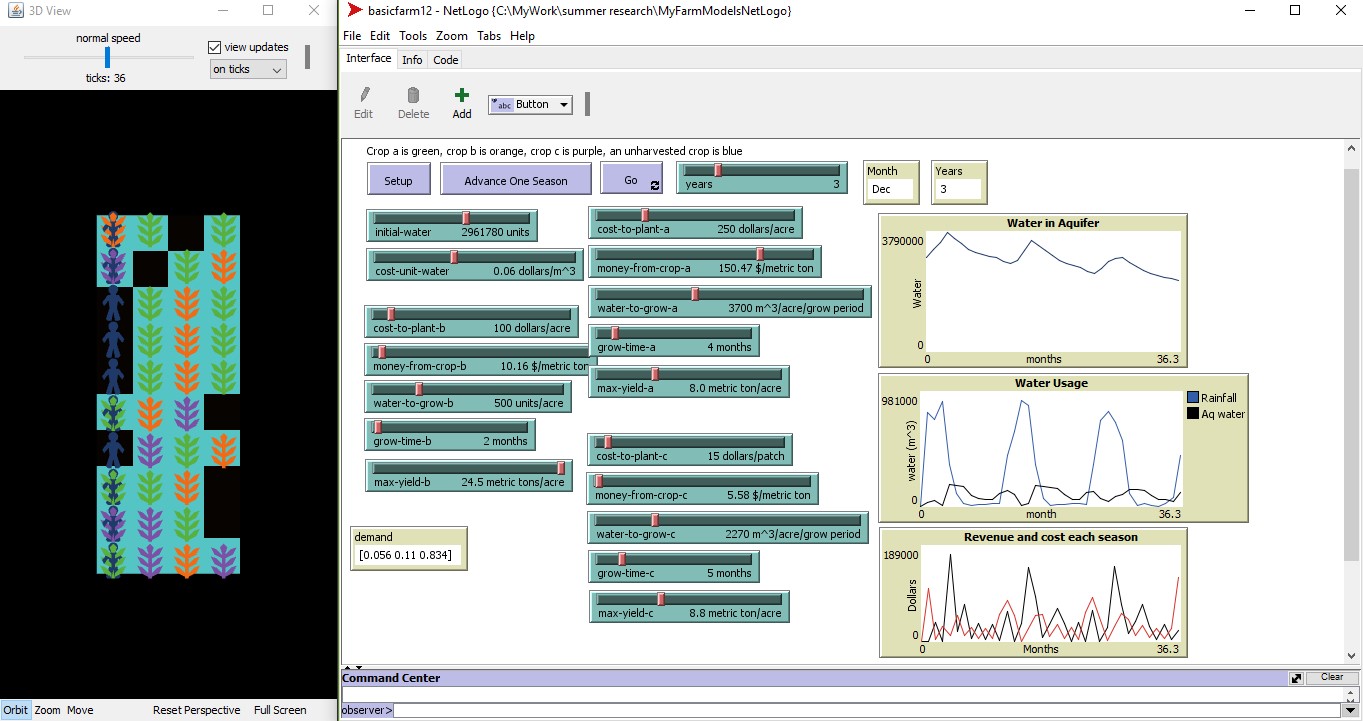
Soft Calculus, Harder Details
Amanda Lipnicki, Alfred University
Abstract: In early 2023, we released a program that automates crochet patterns for surfaces of revolution. We outline mathematics used such as arclength integrals, modular arithmetic, and a variant of the Hausdorff metric. We also explain what led to this work, including examples of artwork created with it, and we indicate some directions for future research. This work is joint with Megan Martinez at Ithaca College.
Spring 2023
Monday, March 27, 2023
5-6 pm
Newton 214
How to Differentiate a Number
Xiao Xiao, Utica College
Abstract: The arithmetic derivative is a function from the set of natural numbers that sends all prime numbers to 1 and satisfies the Leibniz rule (aka as the product rule in calculus). Many unsolved problems in number theory, such as Goldbach's conjecture and twin prime conjecture, can be posed in the context of arithmetic derivative. In this talk, we will survey some elementary properties of the arithmetic derivative and then discuss solutions to two problems on anti-derivatives and higher derivatives in the partial derivative case.
Thursday, February 16, 2023
3-4 pm
Newton 201
Math Talk for Deaf Students
And hearing mathematicians who want to learn some ASL
Carolyn Cronauer, SUNY Geneseo Alumna
Abstract: American Sign Language is a rich, dynamic, and complex language that is constantly evolving to meet the communication and cultural needs of the Deaf community. Math education for D/deaf and hard-of-hearing students is one area that has seen particular growth in recent years. This presentation will discuss trends and challenges in math education for D/deaf students, the value of using ASL as a language for mathematical discourse and pedagogy, and best practices for creating an inclusive and equitable classroom for students with a hearing loss. We will also have some fun learning how to sign common math words and phrases in ASL!
Carolyn Cronauer has taught high school math at Rochester School for the Deaf since 2017. She previously held math teaching positions at various public, charter, and Schools for the Deaf in New York and Ohio. Carolyn has facilitated several workshops on problem based learning and mathematical discourse, including a presentation at the 2018 DEAFTEC National Conference in Austin, Texas. She earned her bachelor’s degree in Mathematics from SUNY Geneseo in 2009, and her master’s degree in Deaf Education from Rochester Institute of Technology in 2011.
Wednesday, March 1, 2023
4-5 pm
Newton 204
Abstract: I claim that the answer to the title question is emphatically "yes," because computer graphics can be an integrative combination of much central material in a typical undergraduate mathematics curriculum, motivated by an intriguing application. I will describe an approach to graphics called "ray tracing," and explore some of the key mathematics it draws on. In particular, I will show the roles that calculus and linear algebra play, supported by a bit of probability, with a couple of important theorems and their proofs, and, of course, an opportunity to practice programming skills. I close by briefly describing an actual course that introduces ray tracing to undergraduate mathematics majors.
Thursday, February 2, 2023
3-4 pm
Newton 201
The Langlands Program: Now and Then
Gary Towsley, SUNY Geneseo
Abstract: The Langlands Program is an effort by mathematicians to elucidate deep connections between "Algebra" and "Geometry." The program began with a set of conjectures by Robert Langlands of Princeton University which he sent to Andre Weil, another mathematician at Princeton, in 1967. The program guides some of the most advanced research in mathematics today.
We will look at three problems from the past (1600s and earlier) which illustrate the connections that the program seeks to reveal.
Fall 2022
Friday, December 2, 2022
3:30-4:20 pm
Newton 204
The cultural context of calculus and the curious complications of convergence
Jeff Johannes, SUNY Geneseo
Abstract: Across the country and world, millions of people are studying calculus right now, just like you are. Why? Because it’s useful? Yes, that’s true. Because it’s interesting? We believe that’s true, even if you don’t as much. How about this … because it is one of the most important and significant accomplishments of humanity? In this talk I will explore this claim - to see what culturally led to the creation of calculus and the societal consequences of calculus. As a demonstration of the interconnectedness of the mathematics, I will explore the history of limits and how they ended up being the most recently developed material that you learn in introductory calculus. Come join us to see why calculus matters.
Friday, November 11, 2022
3:30-4:20 pm
Newton 204
From Geneseo to NC State: A Biomathematical Adventure
Justen Geddes, North Carolina State University
(SUNY Geneseo, Class of 2018)
Abstract: Justen Geddes entered a Ph.D. program at North Carolina State University in 2018. This talk will cover Justen’s thesis research, opportunities for the NCSU Research Experience for Undergraduates (REU), and an overview of the NCSU Biomathematics program.
Justen’s primary research is on Postural Orthostatic Tachycardia Syndrome (POTS), which is characterized by an increase in heart rate of 30 beats per minute upon a postural change, combined with the presence of orthostatic symptoms. We will start by quantifying oscillations and then move into representing these oscillations and dynamics using multi-scale mathematical models that capture potential causes of POTS in the neurons, brain stem, vasculature, and sinoatrial node cell. We will also talk briefly about Justen’s study on neuroscience using methods that are analogous to a higher-order singular value decomposition. We will end the research portion of this talk by examining heart rate variability, a project that was part of the NCSU REU last summer. Justen will then talk about the NCSU REU and Biomathematics program.
Thursday, October 27, 2022
2:30-3:20 pm
ISC 131
This is What Actuaries Do
Madeline Klein, Hannover Reassurance of America
(SUNY Geneseo, Class of 2015)
Abstract: Choosing a career path can be overwhelming, but actuarial science provides many opportunities for those looking for a quantitative field.
At its core, actuarial science is a career path that focuses on quantifying risk. Actuaries are involved in a large number of industries and are in wide demand for many different companies. They use their expertise in statistics to steer the company towards success often aiding senior executives with analysis for better decision making. Primarily, actuaries are found in the insurance industry where they are used to price products, calculate reserves, and provide insight into risk management.
Join Madeline Klein, FSA, to hear more about her experience and career path as she grew from intern to a fellow of a society of actuaries. She will cover:
- An overview of the actuarial field,
- The pathway to pursuing a career in actuarial, and
- Opportunities for an internship at Hannover R
Tuesday, October 18, 2022
4:30-5:20 pm
Newton 204
Ergodicity: from local statistics to global analysis and back
Jenna Zomback, Williams College
(SUNY Geneseo, Class of 2017)
Abstract: Ergodic theory is the study of transformations and group actions on probability spaces; for example, T : [0,1) → [0,1), T(x) = 2x mod 1. A significant part of this theory is occupied by pointwise ergodic theorems, which say that the global analytic behavior of a real-valued function on the space is determined by its local statistics at a random orbit of the transformation/group action, and vice versa. In this talk, we will review transformations on probability spaces by example and discuss the classical pointwise ergodic theorem (due to Birkhoff in 1931). We will also discuss a new pointwise ergodic theorem (Tserunyan--Z. 2020) that features the combinatorics of backward trees in the graph of the transformation.
Friday, October 14, 2022
4:00-5:00 pm
Newton 204
Dynkin diagrams, quaternions, and the "highest root game"
Allen Knutson, Cornell University
Abstract: Given a labeling of a graph by natural numbers, define a "flip" operation replacing a label L by the sum of the adjacent labels, minus L. Say we want to only go up. On what graphs does this process terminate? What are the minimal graphs for which it doesn't?
Answer: (Simply-laced) Dynkin diagrams and affine Dynkin diagrams. These are in correspondence, and I'll correspond them also with finite subgroups of the quaternions. (This connects nicely also to Platonic solids.) Then I'll relate the flipping operation to a corresponding operation on "quiver representations", a very down-to-earth problem in linear algebra.
Tuesday, September 20, 2022
4:30-5:20 pm
Newton 204
How to Leverage Your STEM Education to Succeed in Healthcare IT.
Lisa Smith
Senior Programmer Analyst
Wilmot Cancer Institute
Abstract: “What can I do with a Math Degree?” If I had a nickel for every time I heard that question… Did you know that as a major in STEM, you have skills and knowledge that Healthcare IT needs and wants? Healthcare IT is an exciting, growing field where demand is high and you can build a great career while actually helping people! In addition to technical skills, a STEM education inherently provides graduates with advanced problem-solving and communication skills, excellent time management/prioritization and the ability to take on a multitude of tasks with great focus and determination. By understanding how the language and concepts of Healthcare IT directly translate to terms and concepts you know, demystifying buzz words surrounding data, and creating a road map for next steps that are easily accessible and affordable, we will develop a great answer to: “What can I do with a Math Degree?”
Spring 2022
Wednesday, April 27, 2022
2:30-3:30 pm
Newton 201
Don’t like the universe? Force it to do what you want!
Chris Leary, SUNY Geneseo
Abstract: We investigate various independence results concerning the size of the continuum—how many real numbers there are. In the 1870’s Cantor proved that there are strictly more real numbers than there are natural numbers. But the question of whether there are any infinite sets whose size is strictly between the size of the naturals and the size of the reals was unanswered.
In 1963 Paul Cohen developed the method of forcing and used it to create mathematical models that answered that question. We will give a broad outline of the technique of forcing and indicate how it can be used to determine the size of the continuum.
Tuesday, April 12, 2022
4:00-5:00 pm
Newton 214
Embedding discs and detecting spheres
Arunima Ray, Max-Planck-Institut für Mathematik
(SUNY Geneseo, Class of 2009)
Abstract: One of the central problems in the field of topology is the Poincaré conjecture, which asks how to characterize the n-dimensional sphere, for arbitrary n. This was solved first for n>= 5, then for n=4, and then finally for n=3. I will outline some of the history and mathematics behind the proof in the case n=4. In particular I will explain the features that make this case interesting, and why higher dimensional questions are sometimes easier to solve than lower dimensional ones. The key ingredient is the ability to approximate a continuous function of a disc by one which has no self-intersections.
Wednesday, April 6, 2022
2:30-3:30 pm
Newton 201

Tied up in Knots – An Adventure in Undergraduate Math Research
Aaron Heap, SUNY Geneseo
Abstract: In this lecture, we will discuss what was done in an experimental undergraduate research course in Fall 2021. This will be a math talk that is a knot math talk. We will discuss some knot theory, but we will also discuss some not theory. The not theory portion will involve some knot history, but it will also involve some not history because we will discuss some knot theory from the present. Make sure you are present because those who are not present might miss out on knots but you will not miss out on presents. There will be an occasional knot pun, a smattering of knot fun, and a revelation that the work is not done. This talk should be accessible to a general audience.
Friday, February 11, 2022
4:00-5:00 pm
Newton 204
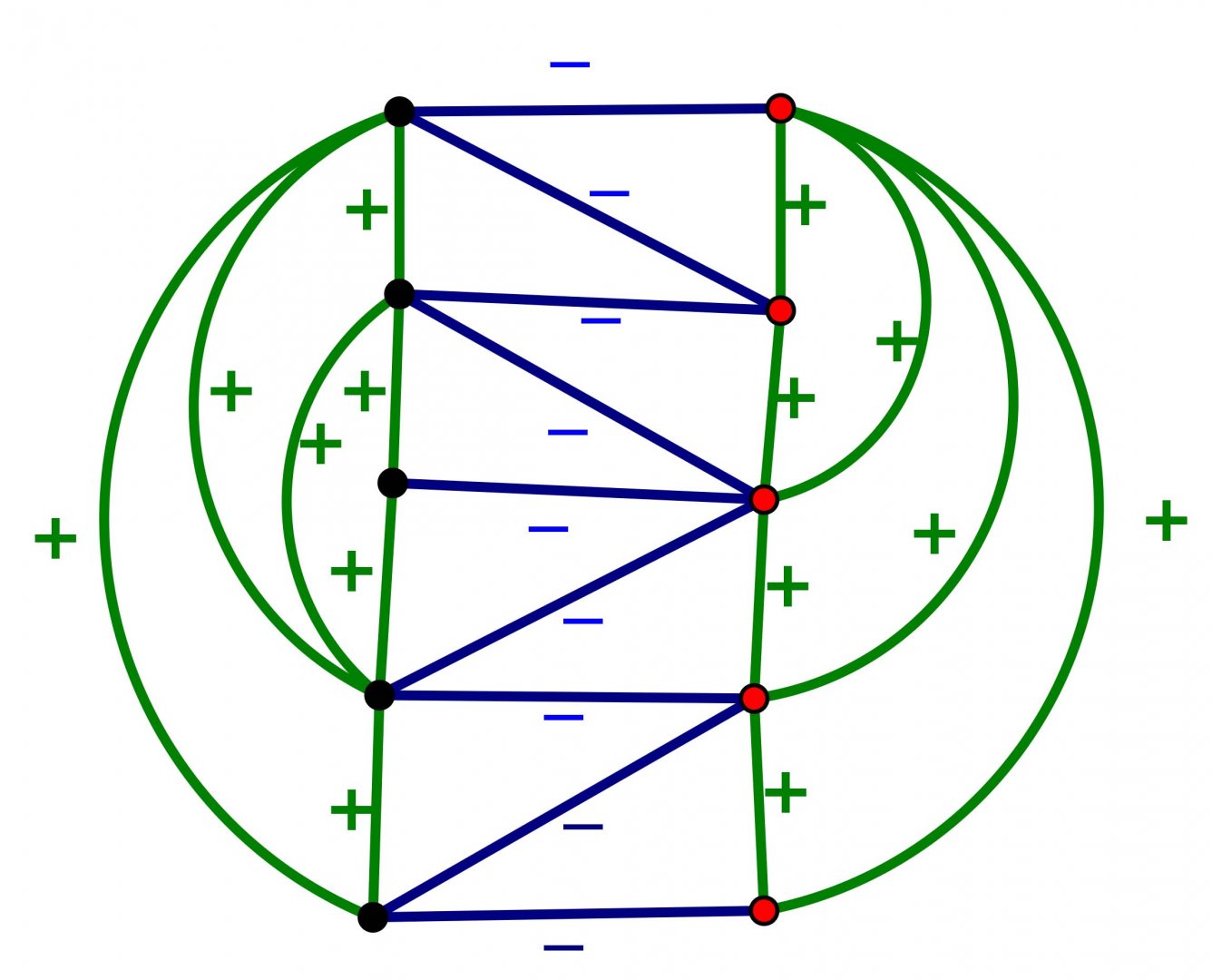
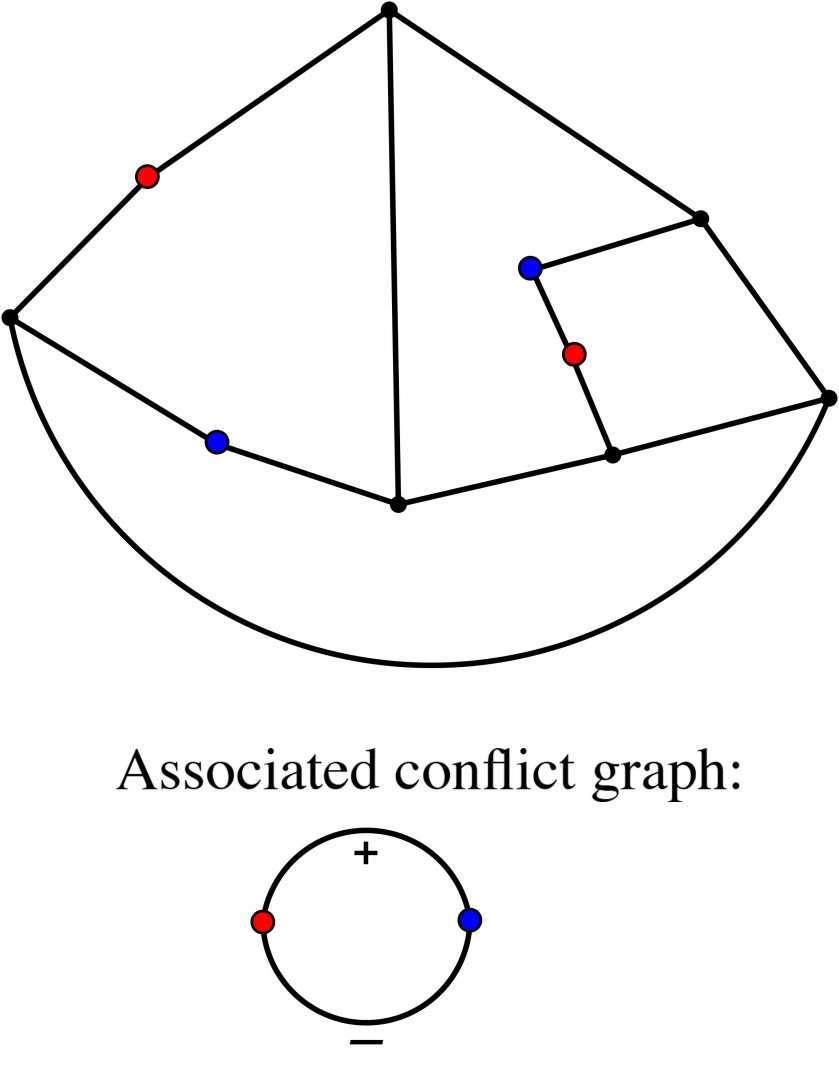
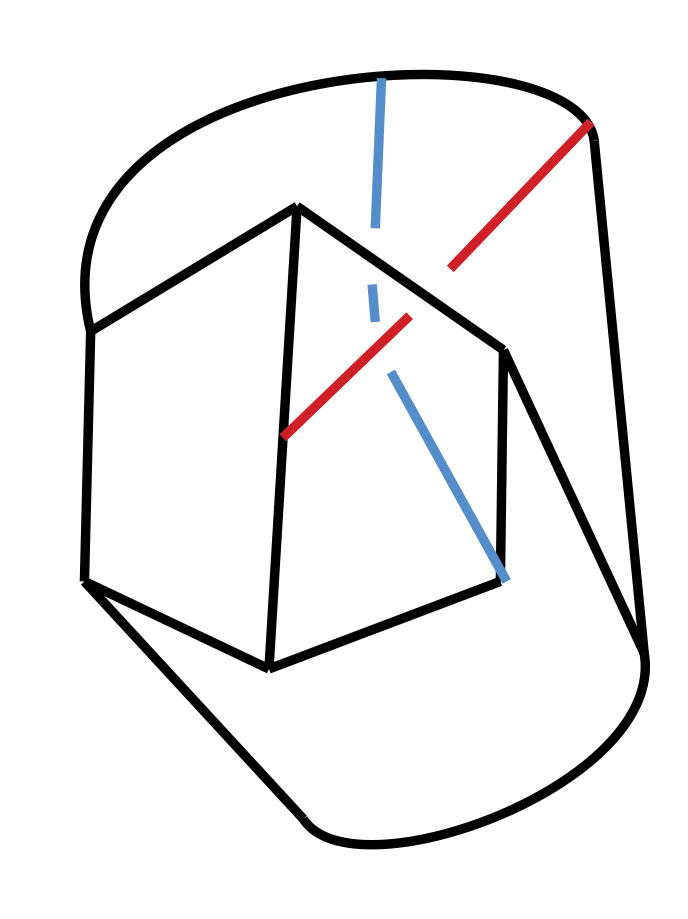
An Introduction to Intrinsically Linked Graphs and to the Conflict Graph
Joel Foisy, SUNY Potsdam
Abstract: A graph is a collection of vertices and edges that connect pairs of vertices. A planar graph is one that can be represented in the plane with vertices as points, edges as arcs, and edges meet only at their endpoints. Tutte's conflict graph (1958) gives one characterization of planar graphs: a graph is planar if and only if the conflict graph of every cycle in G is "bipartite". We discuss an attempt to generalize Tutte's conlict graph to linklessly embeddable graphs in space. A linklessly embeddable graph is a graph that has an embedding in 3-space, and such that no pair of disjoint cycles (circles) form a nonsplit link (one whose components cannot be pulled apart). A graph that is not linklessly embeddable is called intrinsically linked. We will argue that if a graph is intrinsically linked, then the conflict graph associated to all members of certain class of planar subgraphs is "unbalanced" (which is analogous to being nonbipartite).
Fall 2021
Wednesday, November 17, 2021
2:30-3:30 pm
Newton 202
A Concise History of Calculus
Jeff Johannes & Gary Towsley, SUNY Geneseo
Abstract: A lively overview of over two thousand years of calculus history. Not only who-did-what along the way, but the cultural and sociological causes and effects of the calculus. Strongly recommended for anyone who has taken or is taking calculus.
Tuesday, November 9, 2021
4:00-5:00 pm
Newton 201
Hans Christian Andersen and the Pythagorean Theorem
Toke Knudsen, SUNY Oneonta
Abstract: Most people will know at least some of the fairy tales of Hans Christian Andersen (1805–75). They have been translated to some 160 languages and include The Princess and the Pea, The Ugly Duckling, and The Emperor’s New Clothes. But it is not at all well known that Andersen in 1831 wrote a poem, entitled Formens evige Magie ("The Eternal Magic of Form"), which presents the Pythagorean theorem and its proof in poetic form. Polemic in nature, the poem discusses form and substance in poetry, the Pythagorean theorem and its proof used by Andersen as representing strict structural form. The talk will explore Andersen’s recollections of school mathematics and the literary context for his poem about the Pythagorean theorem.
Tuesday, October 26, 2021
4:00-5:00 pm
Newton 201
It’s a Real Problem
Chris Leary, SUNY Geneseo
Abstract: An introduction to the origins and early history of Cantor’s Continuum Problem. Building on the advances and insights into the nature of functions from the early 19th century, Georg Cantor developed, almost singlehandedly, the basis of our understanding of sets and the sizes of sets. He showed that infinite sets come in different sizes, and asked penetrating questions that challenge our perception of the set of real numbers, opening areas of investigation that have been constantly and fruitfully pursued for the past 150 years.
Prerequisites: A general, if vague, understanding of what a real number is. It might be helpful if you have ever used a phone.
Wednesday, September 29, 2021
3:00-3:45 pm
Welles 24

150 Years in the Making: Mathematics Part 2
Gary Towsley, SUNY Geneseo
Abstract: The second of a series of 30-minute presentations on the history and highlights of the Geneseo Mathematics Department. Join Emeriti Professor Gary Towsley for a look at how the Math Department has responded to changes in technology, pedagogy, and the student body and how the department itself has changed.
150 Years in the Making: Mathematics Part 2 - SUNY Geneseo
A video recording of the lecture can be found here. (Passcode: *.kCG5$@)
Wednesday, September 22, 2021
3:00-3:45 pm
Welles 24

150 Years in the Making: Mathematics
Jeff Johannes, SUNY Geneseo
Abstract: The first of a series of 30-minute presentations on the history and highlights of the Geneseo Mathematics Department. Early mathematics at Geneseo was mostly for elementary school teachers and included mathematics taught to the high school population. We will trace the evolution to the time of the liberal arts and secondary major.
150 Years in the Making: Mathematics - SUNY Geneseo
A video recording of the lecture can be found here.
Join Zoom Meeting
https://geneseo.zoom.us/j/88585852975?pwd=bURjbXJ3cDA1MFJIUVR3STZnV2NpQT09
Spring 2021
Wednesday, May 05, 2021, at 4:00-5:00 pm
Emily King, Colorado State University
An Interactive Tour of Some Data Analysis Techniques
Literacy in data analysis techniques is growing more and more important in academia and industry. In this talk, a selection of data analysis techniques --including the basics of neural networks -- will be introduced. The talk will be interactive, so be ready to unmute yourself.
-------------------------------------------------------------------------------------------------------------------
Please click the link below to join the zoom:
https://geneseo.zoom.us/j/95679949369?pwd=dnFMOWxVdHRIVXlJUjNHN1hBYmp5Q…
Passcode: 830844
Wednesday, April 14, 2021, at 4:00-5:00 pm

Picture from Wikipedia
Tuoc Phan, UNIVERSITY of Tennessee-Knoxville.
An invitation to Partial Differential Equations
This lecture is to introduce some fundamental theories on partial differential equations. We begin with the derivation of a general class of reaction-diffusion equations using integration by parts. We then move the study of Laplace equations, which is the simplest class of reaction-diffusion equations. Several important quantitative estimates for solutions of harmonic and Laplace equations will be given. Physical intuition and ideas from calculus will be used to explain these estimates. If time permits, we will also discuss some recent extensions and the development of these results. Prerequisite: Calculus III
-------------------------------------------------------------------------------------------------------------------
Please click the link below to join the zoom:
https://geneseo.zoom.us/j/94212985538?pwd=N0gwTFVqRmhUQ1dLMS9DM3BjbGtZd…
Passcode: 877106
Monday, April 05, 2021, at 4:00-5:00 pm

Carmeliza Navasca, The UNIVERSITY of Alabama at Birmingham
Tensor rank and CP Decompositions via Proximal Algorithms with Applications
First, I will review some tensor basics and tensor decompositions. Specifically, I will discuss the canonical polyadic (CP) decomposition and its challenges. Then, I will discuss some new sparse optimization-based tensor models via proximal algorithms for tensor rank approximation and tensor decomposition. In addition, I will also include numerical examples in surveillance video analysis and matrix/tensor completion as well as model order reduction.
-------------------------------------------------------------------------------------------------------------------
Please click the link below to join the webinar:
https://geneseo.zoom.us/j/96289668676?pwd=UHc3NFplV2JQUWZxSXY5UVVYU0o1U…
Passcode: 102879
Thursday, March 25, 2021, at 4:00-5:00 pm
Nathan Wagner, WASHINGTON UNIVERSITY IN ST. LOUIS
Finite Blaschke Products and Ellipses
In this talk, we will explore a surprising connection between complex analysis (the calculus of functions of a complex variable) and geometry. In particular, we will discuss a beautiful geometric property of finite Blaschke products, which are important building block functions in complex analysis. Finite Blaschke products are rational functions, and thus we may speak of the degree of such a function. It turns out that for any degree-3 Blaschke product, if we connect the three points on the unit circle that the Blaschke product maps to a single unimodular value, and we repeat this procedure for all unimodular values, then we obtain a set of triangles that circumscribe a single ellipse. Interestingly, the foci of this ellipse are precisely the zeros of the Blaschke product! This geometric construction relates to another pretty geometric result known as Poncelet's closure theorem. We will also discuss how a similar result holds true for special kinds of degree-4 Blaschke products.
-------------------------------------------------------------------------------------------------------------------
Please click the link below to join the zoom webinar:
https://geneseo.zoom.us/j/99336614066?pwd=dHBpa0tLT2V3aG1XeUs4aGpLajBUQ…
Passcode: 572600
Wednesday, March 17, 2021, at 4:00-5:00 pm
Anthony Macula, Professor of Mathematics, SUNY Geneseo
Writing Individualized (non-trivial) Math Problems for Online Learning and Testing
The Mobius system is a product of on-line learning company DigitalEd, a subsidiary of the Maplesoft mathematical software company. The Mobius on-line system is vast and allows for a complete presentation of an online course, e.g., embedded videos, guided lessons, homework. It handles latex and mathml. It can be integrated in Canvas. This demonstration/talk/discussion will only focus on the problem generation aspects of Mobius. The system seems ideal for posing math problems from the simple to the sophisticated. The algorithmic language is Maple, a software system that has a plethora of commands written by mathematicians for mathematicians. These commands made it rather intuitive math folk to code individualized multi-part problems for students that can be either algorithmically and/or manually graded. The grading algorithms can be quite powerful.
-------------------------------------------------------------------------------------------------------------------
Please click the link below to join the zoom webinar:
https://geneseo.zoom.us/j/99021133631?pwd=UzNHSWhHWlNCd2Zvdk1XYVFNN2xoZ…
Passcode: 044572
Friday, February 12, 2021, at 4:00-5:00 pm
Monica G. Cojocaru ( Prof. Mathematics, Univ. of Guelph, Ontario, Canada)
Human behavior and regional pandemic control
Students will learn about one of the most used mathematical models (SIR/SEIR) in tracing and interpreting infectious disease spread. In particular, students will learn to analyze a version of this model and relate it to case incidence data for the current pandemic.
-------------------------------------------------------------------------------------------------------------------
https://geneseo.zoom.us/j/99047964736?pwd=Rk1HcGgxVGRoc20xTGU2N0tZUERxQ…
Passcode: 274170
Friday, February 05, 2021, at 4:00-5:00 pm
Jennifer Biermann (Hobart and William Smith Colleges)
Connecting graphs and polynomials
Combinatorial commutative algebra seeks to find connections between algebraic objects (like polynomials) and combinatorial objects (like graphs). This lets us use techniques and results from combinatorics to answer algebraic questions that on the surface don’t seem related. In this talk, I will explain one such connection between polynomials and the edges of a graph called an edge ideal. Then I will talk about how you might generalize this idea, and the difficulties you run into when you do. No background in algebra or graph theory will be necessary to understand the talk.
------------------------------------------------------------------------------------------------------------------------------------
Fall 2020
Tuesday, December 01, 2020, at 4:00-5:00 pm
Left: Schematic of the tear film system. Right: Image of the human tear film with a breakup region highlighted. Original image courtesy of Deborah Awisi-Gyau, Tear Film and Ocular Surface Lab, Indiana University, School of Optometry
Rayanne Luke (Geneseo '16, University of Delaware)
Parameter Identification for Tear Film Thinning and Breakup
Are your eyes ever dry? Hundreds of millions of people worldwide experience dry eye syndrome, which decreases quality of vision and causes ocular discomfort. A phenomenon associated with dry eye syndrome is tear film breakup, or the formation of dry spots on the eye. We fit human tear film data with a hierarchy of simple models to determine which mechanism(s) play a role in causing breakup and estimate breakup parameters that are hard to measure directly. In this talk, I will discuss our results, what they can tell optometrists about tear film function, some limitations of the models, and a promising future direction using machine learning.
------------------------------------------------------------------------------------------------------------------------------------
Please click the link below to join the zoom webinar:
https://geneseo.zoom.us/j/93483414476?pwd=MnNFTy8wVDJCeVU1OGhkNEdEaXE1U…
Passcode: 214574
Thursday, November 19, 2020, at 4:00-5:00 pm
Anthony Macula, Professor of Mathematics, SUNY Geneseo
Making Pooling Designs for COVID-19 Surveillance on a Mass Scale Deployable and Decodable in the Field
This talk describes practical, fieldable, pooled saliva COVID-19 surveillance and diagnostic testing designs that are more efficient than the Dorfman pooling designs widely in use. Symmetry, Geometry, Graph Theory, and Probability come into play. To protect the public from a potential third wave of the COVID-19 pandemic this winter, there may be a need to rapidly increase the volume and rate of both surveillance and diagnostic testing.
------------------------------------------------------------------------------------------------------------------------------------
Please click the link below to join the zoom webinar:
https://geneseo.zoom.us/j/93825210637?pwd=T0h2dTFQaUM4ektOVHVqWlRjVzUzZ…
Passcode: 977878
Tuesday, November 10, 2020, at 4:00-5:00 pm
Thomas Q. Sibley, College of St. Benedict, St. John’s University
Idempotents à la Mod
In ordinary arithmetic has just two solutions,
and
. But in modular arithmetic, we sometimes find more solutions, called idempotents. Come with a pencil and paper for an exploration of patterns and proofs in numbers and algebra.
------------------------------------------------------------------------------------------------------------------------------------
Please click the link below to join the webinar:
https://geneseo.zoom.us/j/91939317471?pwd=cWFoOW9QSW1mak5VdDMraVJTZHJRQ…
Passcode: 442957
Monday, October 26, 2020, at 4:00-5:00 pm
Kathleen Kavanagh, Professor of Mathematics, Clarkson University
Modeling Agricultural Communities with Agent-Based Modeling
There is an increased need for agricultural management tools due to the growing issue of water scarcity. A wide range of simulation and optimization tools have been used to help guide farmers in making decisions. One tool that is rising in popularity is agent-based modeling. In agent-based modeling, each individual agent is able to make their own decisions based on their own behavior rules, making it possible to represent a heterogeneous population. We have begun development of an agent-based model that incorporates multiple competing crops and a decision making process that allows farmers to choose which crop to grow. The model is built in NetLogo to allow for simulations to be run to evaluate the impacts of policy change on the agricultural community.
------------------------------------------------------------------------------------------------------------------------------------
Please click the link below to join the zoom webinar:
https://geneseo.zoom.us/j/92861467083?pwd=a2M0T1d3UXdDOE5aZWNCa1IwaXVOU…
Passcode: 425617
Tuesday, October 13, 2020, at 4:00-5:00 pm
The best picture related to these matrices shows the
Gilbert Strang, Professor of Mathematics, Massachusetts Institute of Technology (MIT)
The Column-Row Factorization
In teaching linear algebra, I usually start with small matrices of integers. It is easy to see the independent and dependent columns of
This factorization makes clear the rank and the column space and the idea of independence and (most of all) the rule for multiplication: Columns of times the submatrix
coming directly from
.
-------------------------------------------------------------------------------------------------------------------
Please click the link below to join the zoom webinar:
https://geneseo.zoom.us/j/
Passcode: 467782
Spring 2020
Wednesday, March 11, 2020, at 2:30-3:30pm
Newton 209

Dr. Nate Barlow, Assistant Professor, School of Mathematical Sciences, Rochester Institute of Technology (RIT)
Asymptotic Approximants
There are several problems of mathematical physics in which the only available analytic solution is a divergent and/or truncated series expansion. Examples include the Post-Newtonian expansion of general relativity, the thermodynamic virial equation of state, and as-of-yet unsolved integrals and differential equations of fluid dynamics (e.g. Blasius boundary layer ODE) and astrophysics (black hole light bending). Over the past decade, a new approach has evolved (which we call Asymptotic Approximants for reasons to be explained) to overcome the convergence barrier in such problems. Simply put, an asymptotic approximant is a closed-form analytic expression whose expansion in one region is exact up to a specified order and whose limit in another region is also exact. The remarkable feature of asymptotic approximants is their ability to attain uniform accuracy not only at the two regions enforced, but also at all points in-between. In this talk, I will demonstrate how to construct an asymptotic approximant via recursion (no matrix inversion required). I will also present a history of the success of asymptotic approximants in providing uniformly accurate analytic solutions to problems of thermodynamics, fluid dynamics, and astrophysics.
Thursday, February 20, 2020, at 2:30-3:30pm
Sturges 109
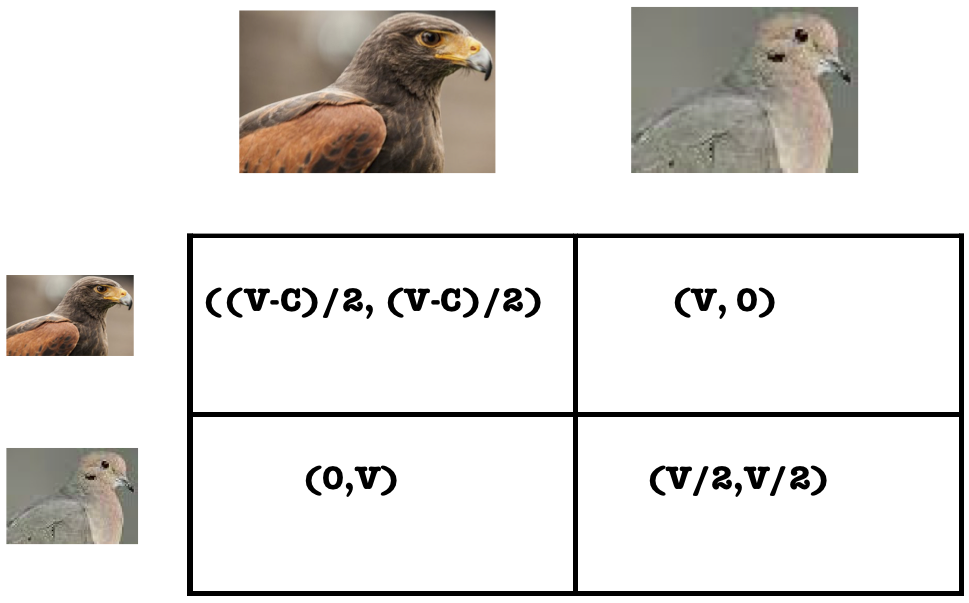
Dr. Ted Galanthay, Associate Professor, Department of Mathematics, Ithaca College
Evolutionary games we play: Hawks, Doves, and More
In the 1960's, ecologists began to use game theory to study evolutionary questions on topics such as animal aggression, the sex ratio, and altruism. Further study led to the genesis of evolutionary game theory which seeks to describe changes in the frequency of strategies over repeated iterations of a game. In this talk, I will introduce evolutionary game theory and describe recent mathematical modeling efforts to integrate population dynamics and evolutionary game theory models to answer questions about the evolution of animal aggression.
Monday, February 10, 2020, at 4:00-5:00pm
Newton 202
Dr. Jonathan Forde, Associate Professor and Chair, Department of Mathematics and Computer Science, Hobart and William Smith Colleges
Mathematical Modeling in Virology
Mathematical modeling is the art and science of describing real-world phenomena in mathematical form. When a model incorporates enough detail of current biological understanding, it can be used in conjunction with other sciences to help interpret experimental results and guide future experiments or policies. In this presentation, I will present mathematical models of viral infections such as hepatitis B and HIV, and the immune responses that protect us from them. We will look at the analytical and numerical methods used to design and validate the models. Some of this work was developed as part of an REU program hosted at Hobart and William Smith Colleges. I will also discuss the REU program, and how to find a research opportunity for this summer.
Friday, February 7, 2020, at 3:30-4:30pm
Newton 203
 Dr. Akhtar Khan, Professor
Dr. Akhtar Khan, Professor
School of Mathematical Sciences, Rochester Institute of Technology (RIT)
Elasticity Imaging Inverse Problem of Locating Cancerous Tumors
Most models in applied and social sciences are given using the broad spectrum of partial differential equations (PDEs) involving parameters that characterize the physical features of the model. For instance, the diffusion coefficient in the Cauchy equation, the rigidity coefficient in fourth-order PDEs emerging from the plate models, and the Láme parameters in linear elasticity describe characteristics of the underlying medium. The direct problem in this context is to solve the PDE or the associated variational problem. By contrast, an inverse problem asks for the identification of the coefficients when a certain measurement of a solution to the underlying direct problem is available. This talk will focus on the elasticity imaging inverse problem of identifying cancerous tumors, which generalizes the practice of palpation by making use of varying elastic properties of healthy and cancerous tissue to locate tumors. More specifically, it is possible, using ultrasound, to measure interior displacements in human tissue (for example, breast tissue). Since cancerous tumors differ markedly in their elastic properties from healthy tissue, the tumors can be located by solving the elasticity. The talk will discuss the underlying mathematical ideas. The outcome of detailed numerical computations carried out using the tissue phantom data will show the efficacy and the feasibility of the developed framework.
Fall 2019
Wednesday, November 20, 2:30-3:45pm
Newton 202
 Dr. Jeff Johannes, Associate Professor of Mathematics and
Dr. Jeff Johannes, Associate Professor of Mathematics and
Dr. Gary Towsley, SUNY Distinguished Teaching Professor of Mathematics
Department of Mathematics, SUNY Geneseo
A CONCISE HISTORY OF CALCULUS
A lively overview of over two thousand years of calculus history. Not only who-did-what along the way, but the cultural and sociological causes and effects of the calculus. Strongly recommended for anyone who has taken or is taking calculus.
Wednesday, October 16, 2019 at 2:30-3:30pm
Newton 201
 Dr. Robert Rogers, SUNY Distinguished Teaching Professor of Mathematics
Dr. Robert Rogers, SUNY Distinguished Teaching Professor of Mathematics
Department of Mathematical Sciences, SUNY Fredonia
Where Am I Ever Going to Use This Stuff?
This talk will present real world applications of mathematics. Topics will include graph theory and theoretical chemistry, divisibility and credit card numbers, prime numbers and internet security, treating kidney stones with ellipses, and, time permitting, complex numbers and airflow.
Wednesday, September 25, 2019 at 2:30-3:30pm
Newton 201
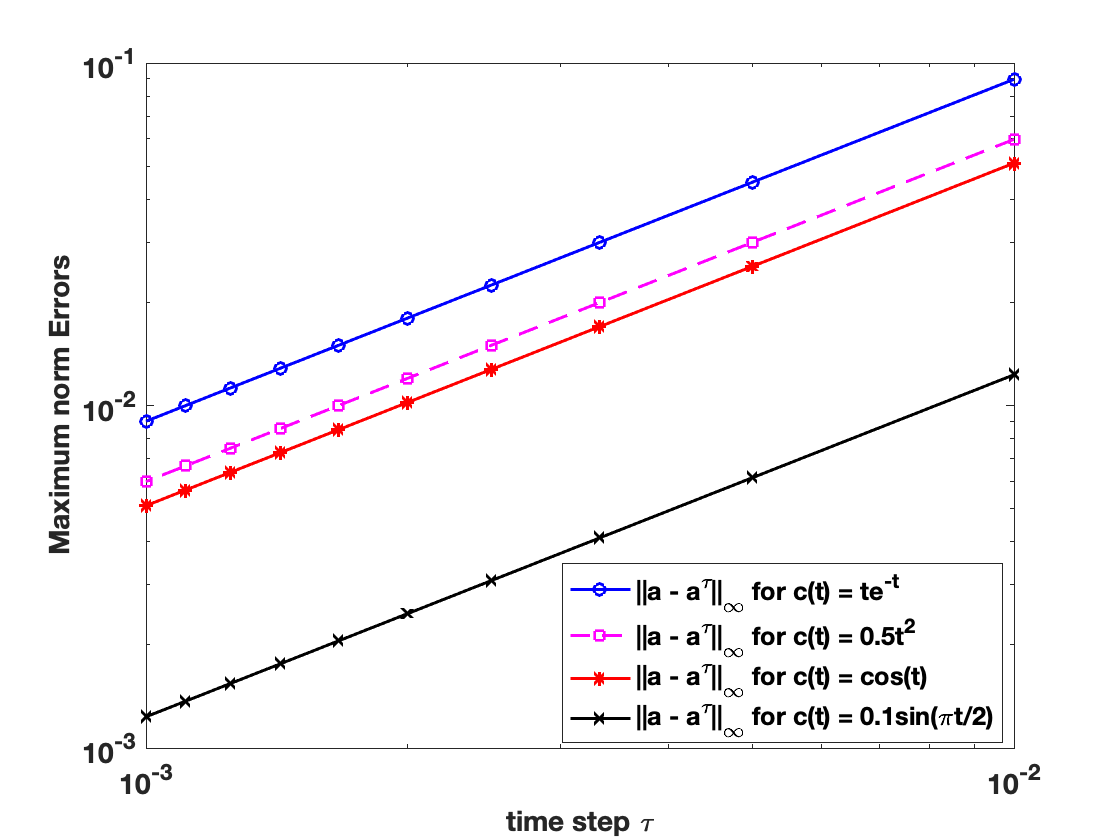 Dr. Sedar Ngoma, Department of Mathematics, SUNY Geneseo
Dr. Sedar Ngoma, Department of Mathematics, SUNY Geneseo
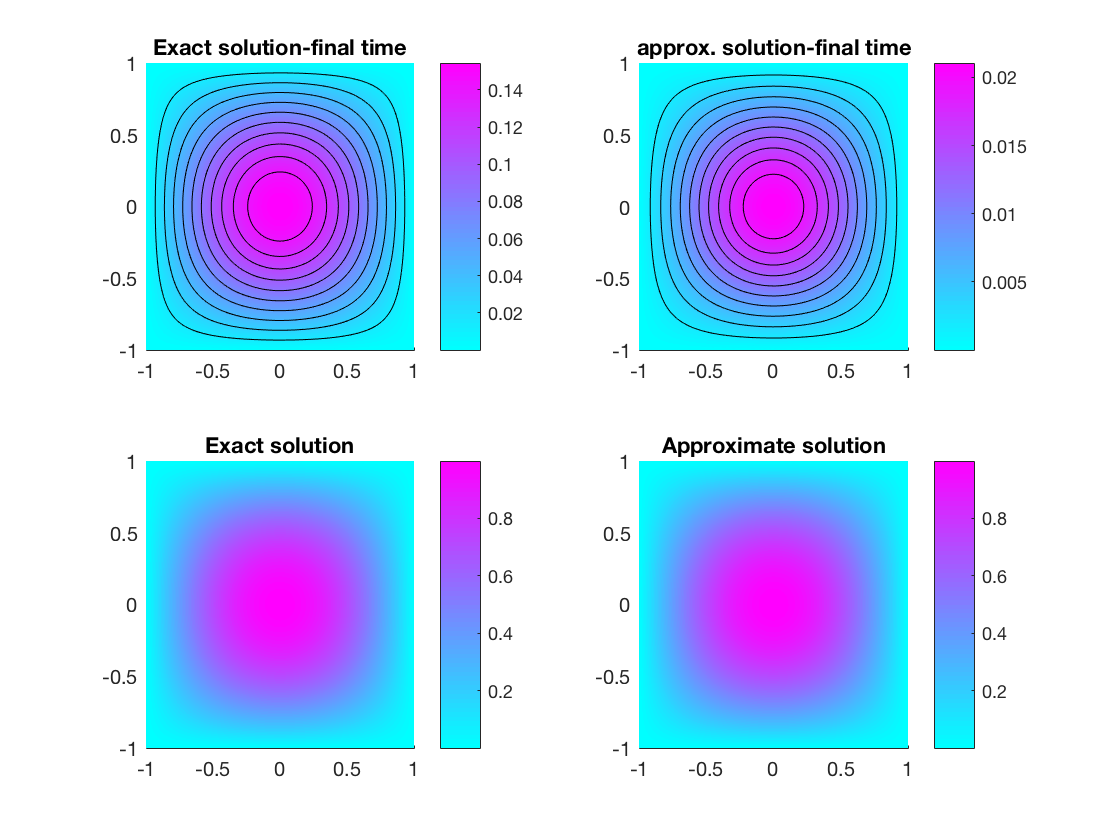
Rate of convergence resulting in a finite difference approximation
Finite difference formulas are incontestably useful for approximating solutions of problems arising from many fields of study, whether the problems come from a real life application or not. However, these formulas give rise to error originating from discretization. In this talk, we recall some basic finite difference formulas and after briefly discussing different types of errors that arise in practical applications, we consider examples to investigate the impact the rate of convergence of a chosen finite difference scheme has on the obtained approximation.
Spring 2019
Thursday, May 2, 2019 at 2:30-3:30pm
Welles 138
Dr. Cesar Aguilar, Department of Mathematics, SUNY Geneseo
Examples in analysis
Every math student has a favorite function that is continuous at every irrational number but discontinuous at every rational number. How about the opposite situation? That is, what is your favorite function that is continuous at every rational number but discontinuous at every irrational number? In this talk, I will present some interesting examples in analysis that are used as counterexamples to natural questions and/or that are used to showcase a newly developed idea. The majority of this talk will be accessible to students having completed Calculus II.
Thursday, April 25, 2019 at 2:30-3:30pm
Welles 138
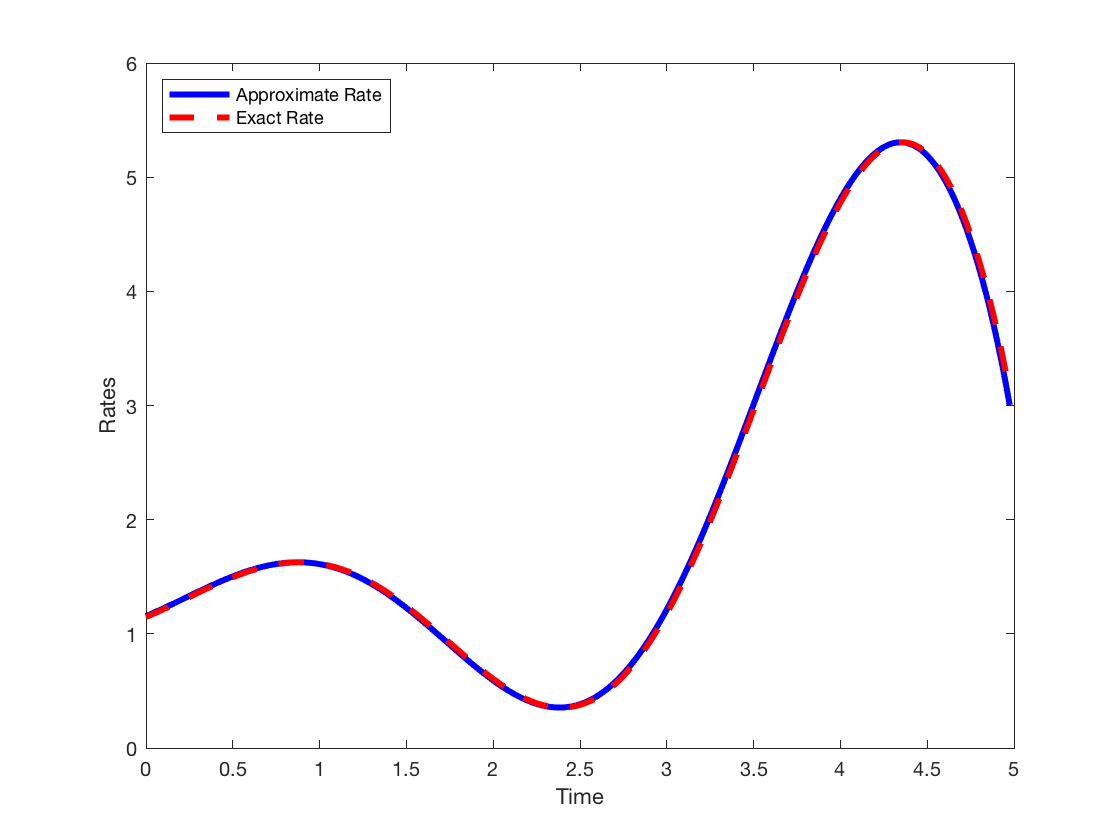 Dr. Sedar Ngoma, Department of Mathematics, SUNY Geneseo
Dr. Sedar Ngoma, Department of Mathematics, SUNY Geneseo
An Introduction to Finite Difference Methods
In applications, when the derivative of a very complicated function f(x) is required, but the process of obtaining it by hand is subject to errors or when the function f(x) is not known explicitly, finite difference methods are employed. For example, finite difference formulas are frequently used in approximating solutions of differential, integral, and integro-differential equations. In this talk, we introduce and motivate simple finite difference schemes, present some applications, and conclude with three GREAT DAY projects solved by our students using a finite difference algorithm.
Thursday, April 18, 2019 at 2:30-3:30pm
Welles 138
 Dr. Stephanie Singer, Data Strategist, Former Chair, Philadelphia County Board of Elections
Dr. Stephanie Singer, Data Strategist, Former Chair, Philadelphia County Board of Elections
Defending Democracy with Mathematics
After holding an election of our own, we will discuss three branches of mathematics that are used in election security and verification. Cryptography can protect ballot privacy. Data analytics can help prioritize investigations. And statistics are used to verify that votes were counted as cast.
Tuesday, April 2, 2019 at 2:30-3:30pm
Welles 138
 Dr. Christopher Leary, Department of Mathematics, SUNY Geneseo
Dr. Christopher Leary, Department of Mathematics, SUNY Geneseo
Learnability can be Undecidable
Netflix suggests movies. Siri is learning your common word usage. Facebook can recognize you in a photo taken at that party that you sort of remember attending, and wish you didn't. Pretty soon machine learning will be helping your doctor, managing your portfolio, and arranging your next blind date.
But what can we prove about how machine learning works and what it can achieve?
We discuss a surprising limitation on our ability to know what machine learning can and cannot do, tying in some set theory and logic along the way.
Prerequisite: An ability to believe six impossible things before breakfast
Wednesday, March 13, 2019 at 4:00-5:00pm
Newton 201
 Marcus Elia, University of Vermont
Marcus Elia, University of Vermont
Fast Polynomial Multiplication for Cryptography
Some modern public key cryptosystems require multiplication of polynomials with several hundred terms. The efficiency of encryption and decryption depends on having a multiplication algorithm that is optimized for a specific degree. Recently, researchers have suggested using a modification of the Toom-Cook algorithm. However, rigorous mathematics is needed to formally state how the algorithm works when the polynomial coefficients are multiplied modulo a power of two. In this talk, I will introduce the Toom-Cook algorithm and develop the theory necessary to apply it to polynomials for cryptography. This will involve the discussion of computational complexity, combinatorial identities, and number theory.
Friday, February 1, 3:30-4:30pm
Newton 214
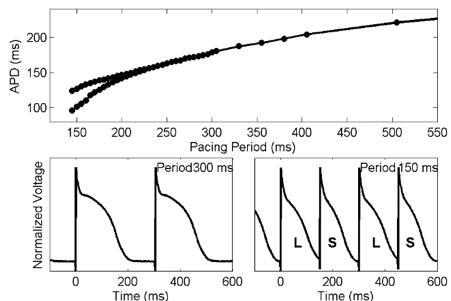 Dr. Elizabeth Cherry, Rochester Institute of Technology (RIT)
Dr. Elizabeth Cherry, Rochester Institute of Technology (RIT)
Computational Modeling of Electrical Dynamics in the Heart
The heart is an electro-mechanical system in which, under normal conditions, electrical waves propagate in a coordinated manner to initiate an efficient contraction. In pathologic states, known as cardiac arrhythmias, single and multiple rapidly rotating spiral waves of electrical activity can appear and generate complex spatiotemporal patterns of activation that inhibit contraction and can be lethal if untreated. Studying the mechanisms responsible for disruption of cardiac wave propagation experimentally is difficult for many reasons, including limited access to quantities of interest and biological variability. Mathematical modeling of cardiac electrical wave propagation can overcome these obstacles but presents a new set of challenges. In this talk, I will discuss the basics of cardiac arrhythmias as well as some experimental techniques to study them. I will show how mathematical models based on differential equations can be used to describe the propagation of electrical waves in cardiac tissue as well as how these models can be solved computationally, along with limitations to this type of approach. Finally, I will give examples of how mathematical modeling can help to elucidate the dynamics of cardiac arrhythmias.
Thursday, January 24, 4:00-5:00pm
Newton 203
Dr. Joseph Rusinko, Department of Mathematics and Computer Science, Hobart and William Smith Colleges
Mathematical Phylogenetics: A summer research possibility
Mathematical Phylogenetics describes a wide range of mathematical and computational tools scientists use to understand evolution. Former SUNY Geneseo students participated in NSF-funded Research Experiences for Undergraduates working on two such questions. 1) If two scientists propose different trees to describe the evolutionary history of a collection of organisms, what mathematical tools can help measure the difference between those descriptions? 2) Given a collection of DNA sequences associated to a set of similar looking individuals, how do we determine how many different species are represented in this group? We will discuss their findings as well as tips for applying to mathematics REU programs this summer.
Fall 2018
Wednesday, December 5, 4:00-5:00pm
Newton 203
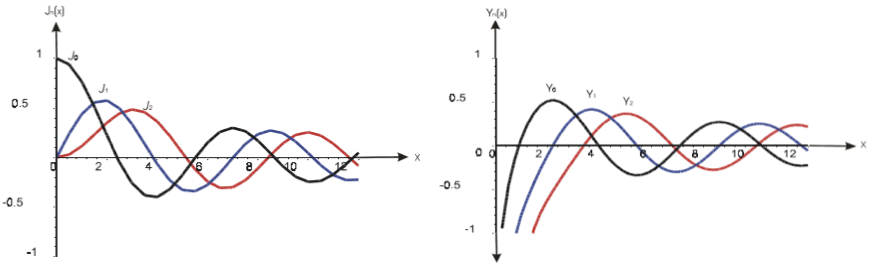 Dr. Ahmad Almomani, SUNY Geneseo
Dr. Ahmad Almomani, SUNY Geneseo
Bessel Integrals
Bessel Functions are among the most important special functions, having diverse applications to physics, engineering and mathematical analysis itself. In particular, the integral representations for the product of Bessel functions are useful for evaluating definite integrals that contain products of two Bessel functions under the integral sign. In addition, they may be considered as a natural generalization of well-known trigonometric identities like $\sin^2(x) + \cos^2(x) = 1$. Some known integral representations for the product of two Bessel functions of the same argument and same order, one of which is Nicholson's formula, which expresses the sum $J^2_{\nu}(x) + Y^2_{\nu}(x)$ as an integral over a hyperbolic Bessel function.
Thursday, November 29, 2:30-3:30 pm
Newton 203
 Dr. Jessalyn Bolkema, SUNY Oswego
Dr. Jessalyn Bolkema, SUNY Oswego
Errors, Eavesdroppers, and Enormous Matrices
Join us for a tour of the mathematics of information security. Cryptography aims to protect information from malicious eavesdroppers. Coding theory aims to protect information from inadvertent errors - consequences of a noisy environment. These are two very different problems - but amazingly enough, solutions to one problem can be used to build solutions to the other. We'll talk through some fundamental principles and key ideas in both coding theory and cryptography, with an end goal of appreciating their intersection: the future of post-quantum security.
Monday, November 19, 2:30-3:30 pm
Newton 203
 Marcus Elia, University of Vermont
Marcus Elia, University of Vermont
NTRU: An Example of a Quantum-Resistant Public Key Cryptosystem
Public key cryptography is used to securely send messages, but many widely-used cryptosystems will be broken if large quantum computers are successfully built. Over the past two decades, researchers have proposed many cryptosystems that currently cannot be broken in classical or quantum polynomial time. In this talk, I will summarize the concept of public key cryptography, describe the RSA cryptosystem, and introduce the NTRU cryptosystem.
Wednesday, November 14, 2:30-3:45pm
Newton 202
 Dr. Jeff Johannes and Dr. Gary Towsley, SUNY Geneseo
Dr. Jeff Johannes and Dr. Gary Towsley, SUNY Geneseo
A CONCISE HISTORY OF CALCULUS
A lively overview of over two thousand years of calculus history. Not only who-did-what along the way, but the cultural and sociological causes and effects of the calculus. Strongly recommended for anyone who has taken or is taking calculus.
Friday, October 19, 2:30-3:30pm
Newton 204
 Dr. William Cipolli, Department of Mathematics, Colgate University.
Dr. William Cipolli, Department of Mathematics, Colgate University.
A user-friendly approach to supervised learning.
I will discuss a classification model that extends Quadratic Discriminant Analysis (QDA) and Linear Discriminant Analysis (LDA) to the Bayesian nonparametric setting, providing a competitor to MclustDA. This approach models the data distribution for each class using a multivariate Polya tree and the flexibility gained from further relaxing the distributional assumptions of QDA can greatly improve performance when severe deviations from the parametric distributional assumptions are present, while still performing well when the assumptions hold.
Tuesday, September 18, 4:00-4:50pm
Newton 203
BethAnna Jones, SUNY Geneseo
This is Your Brain on Math: The Mathematics of Tracking Neurons
Modern imaging methods allow us to view the activity of tens of thousands of neurons in the brain. However, due to the large number of images to sort through, manual methods of location, identification, and analysis of these individual neurons is tedious and time-consuming. Researchers need an automated system to complete in hours what may take an expert weeks or even years. Some automated computer techniques exist, but they find only roughly half the cells, and disagree on half of what they find. Current leading methods analyze neural images using singular value decomposition and constrained non-negative matrix factorizations. We will compare the cells identified with these methods and improve them by i) developing new statistical criteria for identifying cells; ii) investigating correlation patterns across cells; and iii) aligning cells between recording sessions in order to compare cell activity across days.
Eric Piato, SUNY Geneseo
Exploring Graph Theory: Preliminaries, Algebra, and the Eigenvalues of anti-regular graphs
What do network engineering, biological systems, knots, and chemical bonding have in common? All four fall in the breadth of disciplines modeled using graph theory. We begin this talk by exploring the intuition, and some of the formalities, behind key components of graph theory. We move on to consider graphs from a linear-algebraic perspective, introducing the eigenvalues of graphs. We discuss our summer research involving a particular class of graphs, and our attempt to find expressions for the eigenvalues of these graphs. We conclude by briefly describing the results obtained in our publication, Spectral characterizations of anti-regular graphs.
Spring 2018
Thursday, April 26, 2:30-3:30pm
Newton 203
 Ahmad Almomani, SUNY Geneseo
Ahmad Almomani, SUNY Geneseo
Particle Swarm Optimization
Derivative-free methods are highly demanded in the last two decades for solving optimization problems. Derivative-Free Optimization (DFO) are applicable for these problems where the derivatives are not available or hard to compute. The growing demand for sophisticated DFO methods has motivated the development of a relatively wide range of approaches. In this talk, I will introduce Particle Swarm Optimization (PSO) as a DFO method for global optimization with general nonlinear constrained, as a classical penalty and barrier methods, and filter method. In addition, unsupervised PSO introduced and compared with PSO on many test problems. Numerical results and many applications introduced.
Thursday, March 22, 2:30-3:30pm
Newton 203
 Sedar Ngoma, SUNY Geneseo
Sedar Ngoma, SUNY Geneseo
An overview of inverse problems
When solving (or approximating solutions of) problems in science, engineering, mathematics, and many other fields, a process called a model is described in detail and an appropriate input called a cause is supplied. One is then required to find the unique output (or solution) called effect. This is known as direct or forward problems. In direct problems the media properties of a given model described by equations (for example, equation coefficients) are assumed to be known. However, media properties are often not readily observable. This lack of specification in the model leads to inverse problems, in which one is required to find the cause of the effect given the effect. For instance, one can try to determine the equation coefficients (which usually represent important media properties) from the information about solutions of the direct problem. One of the drawbacks of inverse problems is that their (approximate) solutions are almost always ill-posed in the sense that they may not be unique or stable. In this talk we introduce inverse problems, investigate some examples, and describe analytically and numerically a regularization technique used to combat instability in the solutions.
Friday, February 16, 2:30-3:30pm
Newton 203
 Billy Jackson, SUNY Geneseo
Billy Jackson, SUNY Geneseo
From Differential Equations to Difference Equations
and Everything Else in Between
Of all areas of modern mathematics, differential equations is perhaps one of the oldest, of course going back to the days of Leibniz and Newton. Mathematicians in the latter half of the 20th century also began examining difference equations in detail as these structures became important in numerically solving differential equations with the advent in computing that took place. There are many similarities between discrete and continuous dynamical systems, but there are often many differences as well. For example, solutions to the usual logistic equation can exhibit chaotic behavior in discrete systems while simultaneously not being chaotic in their continuous counterparts.
In 1988, a German mathematician by the name of Stefan Hilger constructed a framework that we now call analysis on time scales which explains the similarities and differences between the two extremes: in addition to this unification aspect, we can now extend the analysis to other dynamical systems as well. For example, systems containing hybrid continuous and discrete components, fractal structures, or non-uniformly spaced domains are all ripe for exploration within this framework that will allow for a single analysis to treat them all.
In this talk, I will present Hilger's framework and then discuss applications of the work in one of my recent projects focusing on stability analysis and control theory from an engineering perspective. Most details will hopefully be accessible to those with at least a slight background in differential equations and an adequate preparation in analysis.
Thursday, February 1, 2:30-3:30pm
Newton 203
 Yesim Demiroglu, University of Rochester
Yesim Demiroglu, University of Rochester
Waring's Problem over Finite Fields
Since Edward Waring stated his famous conjecture in his book "Meditationes Algebraicae" in 1770, Waring's problem has been of particular interest to mathematicians. As Charles Small put it in his survey "Indeed, it is one of those nasty gems, like Fermat's Last Theorem, which begins with a simply-stated assertion about natural numbers, and leads quickly into deep water.". The first half of our journey will be a quick introduction to Waring's problem in its original form together with its variants and a summary of some of the results in the literature. The second half of the talk is devoted to our contribution to this problem, namely how one can use Cayley digraphs and graph theoretical methods to solve Waring's problem over finite fields.
Friday, January 26, 2:30-3:30pm
Newton 214
 Pamela E. Harris, Williams College
Pamela E. Harris, Williams College
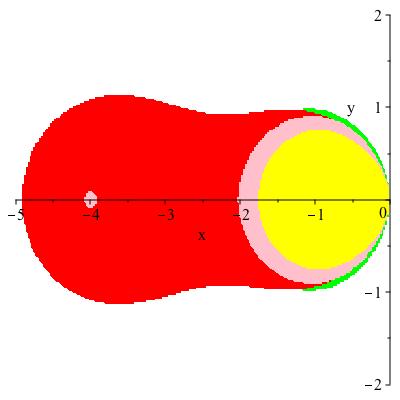
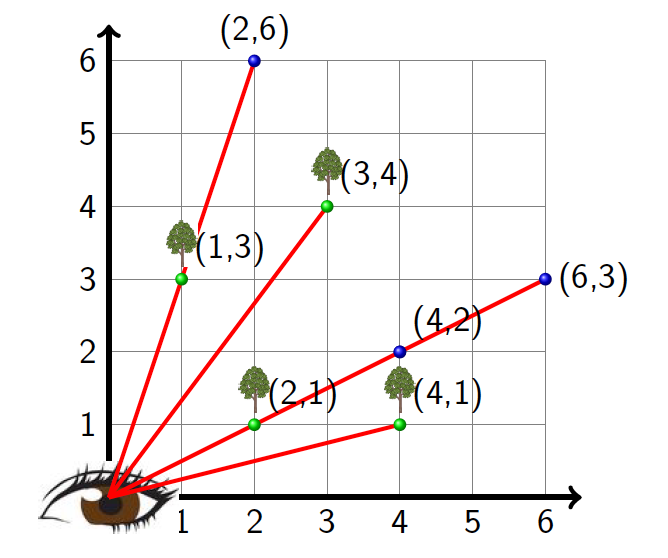
Invisible Lattice Points
This talk is about the invisibility of points on the integer lattice Z x Z, where we think of these points as (infinitely thin) trees. Standing at the origin one may notice that the tree at the integer lattice point (1, 1) blocks from view the trees at (2, 2), (3, 3), and, more generally, at (n,n) for any positive integer n. In fact any tree at (l,m) will be invisible from the origin whenever l and m share any divisor d, since the tree at (l/D,m/D), where D = gcd(l, m) blocks (l, m) from view. With this fact at hand, we will investigate the following questions. If the lines of sight are straight lines through the origin, then what is the probability that the tree at (l, m) is visible? Meaning, that the tree (l, m) is not blocked from view by a tree in front of it. Is possible for us to find forests of trees (rectangular regions of adjacent lattice points) in which all trees are invisible? If it is possible to find such forests, how large can those forests be? What happens if the lines of sight are no longer straight lines through the origin, i.e. functions of the form f(x) = ax with a ∈ Q, but instead are functions of the form f(x) = ax^b with b a positive integer and a ∈ Q? Along this mathematical journey, I will also discuss invisibility as it deals with the underrepresentation of women and minorities in the mathematical sciences and I will share the work I have done to help bring more visibility to the mathematical contributions of Latinx and Hispanic Mathematicians. Math work is joint with Bethany Kubik, Edray Goins, and Aba Mbirika. Diversity work with Alexander Diaz-Lopez, Alicia Prieto Langarica, and Gabriel Sosa.
Fall 2017
Friday, December 1, 2:30-3:30pm
Newton 214
 Joshua Hallam, Wake Forest University
Joshua Hallam, Wake Forest University
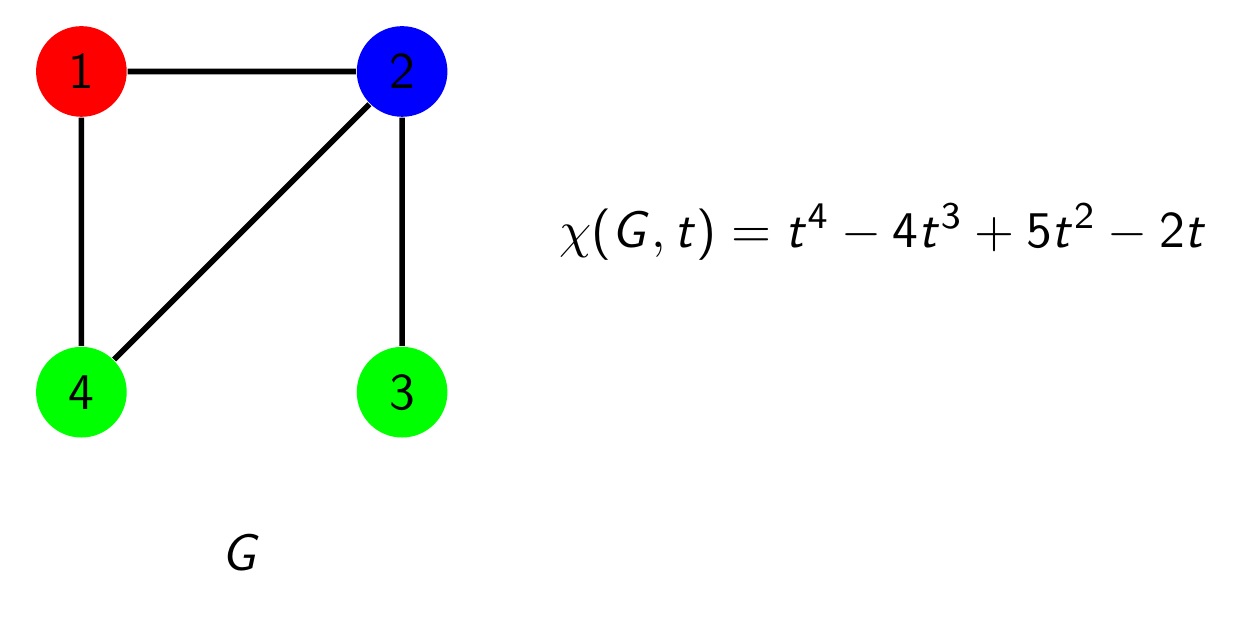
Graph Coloring and Counting Increasing Forests
One of the most famous problems in combinatorics is the four color problem. It asks the following. Given any map, for example a map of the states of a country, is it always possible to color the map with at most 4 colors so that no two states that share a border are colored with the same color? In 1912 George Birkhoff introduced the chromatic polynomial as a tool to try to solve this problem. Although it was not used in the proof of the four color theorem, the chromatic polynomial has many remarkable properties. In this talk, we will discuss the chromatic polynomial and see a surprising connection between its coefficients and objects called increasing forests. I will also discuss some of the research two undergraduate students conducted with me over the summer related to this work and discuss some open problems.
Monday, November 27, 4:00-5:00pm
Newton 201
 Colby Long, Mathematical Biosciences Institute,
Colby Long, Mathematical Biosciences Institute,
the Ohio State University
Reconstructing the Past with Math: Evolutionary trees from
DNA sequences
Understanding the evolutionary relationships between species is vitally important for species conservation, epidemiology, and evolutionary biology. With modern gene-sequencing techniques, we now have access to copious amounts of DNA sequence data. The field of phylogenetics is focused on turning this data into phylogenetic trees, graphs that explain how species have evolved and how they are related. In this talk, we will explore some of the novel mathematical ideas used in phylogenetics to extract evidence of the past from DNA sequences. We will also discuss some of the challenges and open problems for future mathematicians in the field.
Monday, November 20, 4:00-5:00pm
Newton 201
 Jamie Juul, Amherst College
Jamie Juul, Amherst College
The Birthday Problem and a Problem in Arithmetic Dynamics
In a group of n people, what is the probability that two people share a birthday? Suppose we have a function mapping from a set S with d elements back to itself. If we pick a point from the set and apply the map over and over again what is the probability that we eventually return to the point we started with? The first question is the classical birthday problem, the second is a question from arithmetic dynamics. We will discuss these questions and how they relate to each other.
Thursday, November 16, 4:00-5:00pm
Newton 203
 Katelynn Kochalski, SUNY Cortland
Katelynn Kochalski, SUNY Cortland
An Introduction to Queueing Theory
Have you ever wondered how grocery stores decide the number of cashiers to staff on a Sunday afternoon? Or how the TSA determines the number of agents needed during a given shift? These questions both relate back to queueing theory. This talk will explore some basic concepts in queueing theory. In particular, we will investigate properties of a queue where key characteristics of each customer are given in a random but suitably nice fashion. This will allow us to make predictions about the number of customers in the queue and the length of time each customer will be in the system using our knowledge of Calculus II in a surprising way.
Wednesday, November 15, 2:30-3:45pm
Newton 204
Jeff Johannes and Gary Towsley, SUNY Geneseo
A CONCISEHISTORY OF CALCULUS
A lively overview of over two thousand years of calculus history. Not only who-did-what along the way, but the cultural and sociological causes and effects of the calculus. Strongly recommended for anyone who has taken or is taking calculus.
Thursday, November 2, 4:00-4:50pm
Newton 203
 Raymond Cook, AIR Worldwide
Raymond Cook, AIR Worldwide
Introduction to Catastrophe Modeling
In the case of rare but severe events, historical loss information and traditional actuarial methods are inadequate for assessing future loss potential. AIR Worldwide developed probabilistic models that help organizations prepare for the financial impacts of catastrophes—before they occur. These probabilistic models are effectively robust Monte Carlo simulations of how catastrophe losses might develop over the next 12 months. In this talk, I will discuss why catastrophe modeling is an integral part of the insurance industry and introduce a few key concepts in catastrophe modeling.
Thursday, October 19, 4:00-4:50pm
Newton 203
Yusuf Bilgic, SUNY Geneseo
The mathematics behind emerging data science and machine learning
Statistics, mathematics, data management and computer programming have been merged in the practices of data science and machine learning, two growing interdisciplinary sciences. The talk covers technical and nontechnical discussions about some of the new developments in data science and machine learning in the data era through the window of a statistician who works at a mathematics department and has designed a machine learning course. Putting aside brilliant career opportunities for applied mathematicians and statisticians who are excelled with the toolboxes in data and algorithmic modeling, I emphasize that the strong foundation of mathematics plays the pivotal role in the data era. In this talk, I will share some mathematical details about three “winner” algorithms for classification, Linear Discriminant Analysis (LDA), Neural Networks (NN) and Support Vector Machines (SVM). I will also attempt to predict the next 50 years of the directions of data and algorithmic modeling without using any winner algorithms.
Thursday, September 28, 4:00-4:50pm
Newton 203
Dane Taylor, University of Buffalo
Centrality Analysis for Time-Varying Social Networks (and Beyond)
Many datasets are naturally represented by networks in which nodes represent objects and edges represent connections between the objects. Some examples include persons connected by friendships, neurons connected by axons, and webpages connected by hyperlinks. Given a network, an important problem is “centrality analysis” in which the goal is to identify how central (i.e., important) each node is. Centrality in social networks, for example, can reveal which persons are most important and/or influential. One of the leading approaches to centrality is Google’s PageRank algorithm, which identifies the most important webpages on the internet and has also been applied to diverse datasets ranging from gene-correlation networks to Facebook friendships. While there are many methods for centrality analysis, how to study networks that change over time has remained problematic. I will describe some of the relevant issues and present an approach we recently developed for a broad class of centralities known as eigenvector centrality. Using this approach, I will explore a few applications including data analytics for the Mathematics Genealogy Project, actor co-starring during the Golden Age of Hollywood, and citations between Supreme Court Decisions.
Spring 2017
Monday, April 17, 2:30 pm
Newton 203
Katie Gayvert, Weill Medical College, Cornell University
Precision Medicine in the Age of "Big Data": Leveraging machine learning and Genomics for drug discoveries
Over the past few decades, great strides have been made in the treatment of cancer through the adoption of precision medicine approaches. One major effort of precision medicine is the greater application of targeted therapies, which seek to selectively kill tumor cells. However there are many challenges associated with the development and application of these therapies, including identification of tractable targets and the inevitable development of drug resistance. Furthermore the clinical trial failure rate continues to rise, which remains a barrier in the development of novel targeted therapies. Integration of extensive genomics datasets with large drug databases allows us to begin to address these problems. To this end, we have leveraged machine learning and “Big Data” to develop in silico drug discovery and toxicity prediction methods. I will give an overview of the predictive models developed in our lab and the underlying mathematical models that they employ. Approaches such as these have the potential to make a direct impact on how patients are treated, as well as to help prioritize and guide additional focused studies.
Wednesday, April 13, 2:45 pm
Newton 203
Robert Stephens, SUNY Geneseo
QUATERNIONS AND NUMBER SYSTEMS
The scene will be set by looking at the properties of familiar number systems like, for example, integers, rational numbers, and complex numbers. We then introduce the quaternions, which are an extension of the complex numbers. Some of the algebraic properties and uses of the quaternions will be discussed. One such use is calculating the rotation of objects, such as computer generated objects. Euler angles are another way to rotate objects, and we will see some of the difficulties that can arise. If time permits, we will extend the quaternions to new number systems, each of which have their own interesting algebraic properties.
Friday, April 7, 2:30 pm
Newton 203
Chad Magnum, Niagara University, Lewiston, NY
STRUCTURE AND SYMMETRY: AN INTRODUCTION TO LIE ALGEBRAS AND REPRESENTATION THEORY
Mathematical structure and symmetry have long fascinated the human mind. An in-depth study of these topics has helped to lead to quite a bit of the modern mathematical and scientific sophistication we enjoy today. One manifestation of this study is Lie algebra representation theory, which has been significant in various areas of mathematics and physics for several decades. In this talk, I will discuss how one can view Lie algebra representation theory from a perspective which is grounded in natural intuition of structure and symmetry. It is my hope that this discussion gives the audience a taste of the topic, provides context for how to demystify a potentially daunting subject, and stimulates enthusiasm for this fascinating field of mathematics.
Thursday, March 23, 2:30 pm
Newton 203
Ahmad Almomani, Clarkson University, Potsdam, NY
DERIVATIVE-FREE METHODS AND APPLICATIONS
Derivative-free methods are modern techniques used to solve optimization problems. In many practical applications the derivatives are not available or hard to compute due to a “black-box” or simulation-based formulation. Derivative-Free Optimization (DFO) methods are applicable for these kinds of problems as opposed to methods that employ derivatives. The need for DFO arises extensively across all engineering disciplines. In this talk, we compare and analyze the performance of different solvers for local and global optimization paired with different constraint handling techniques (penalty, barrier, and filter methods). Specifically we consider implicit filtering (IF), Nelder-Mead (NM), DIRECT (DIR), a genetic algorithm (GA), particle swarm optimization (PSO), and simulated annealing (SA). We use different values of the penalty or barrier parameters on both smooth and noisy problems. By using performance and data profiles together with a convergence test that measures the decrease in objective function value, we seek to identify which is the best solver and constraint method on which kind of optimization problem. We also hybridize the implicit filtering algorithm with the filter method for constraints to get a new algorithm. Additionally, we introduce a new algorithm that combines the filter method with PSO. We apply the new algorithms for local and global optimization on a Hydraulic Capture Problem from environmental engineering and a suite of test problems and show the new methods are competitive compared with classical approaches for handling constraints.
Thursday, March 2, 2:30 pm
Newton 203
Eleni Panagiotou, UC Santa Barbara, Santa Barbara, CA
QUANTIFYING ENTANGLEMENT IN PHYSICAL SYSTEMS
Many physical systems, such as biopolymers and polymer melts, are composed by macromolecules which cannot cross each other and attain entangled conformations. The entanglement complexity in these systems affects dramatically their mechanical properties. For their simulation, Periodic Boundary Conditions (PBC) are employed, which impose further complications. In this talk we will see methods by which one can measure entanglement in collections of open or closed curves in 3-space and in systems employing PBC. More precisely, using the Gauss linking number, we define the periodic linking number as a measure of entanglement for two oriented curves in a system employing PBC and study its properties. We will see two applications of these measures. First, we will apply our entanglement measures to discuss the evolution of the dimensional character of the entanglement as a function of density in Olympic systems which model the behavior of DNA networks. Next, using Molecular Dynamics simulations, we will apply our measures to investigate how the entanglement of polymeric chains relates to bulk viscoelastic responses in polymeric materials. Our approaches provide new mathematical tools for characterizing the origins of the rheological responses of polymeric materials.
Monday, February 27, 2:30 pm
Newton 203
Yu-Min Chung, College of William and Mary, Williamsburg, VA
COMPUTATIONAL TOPOLOGY WITH APPLICATIONS IN THE NATURAL SCIENCES
Computational topology is a relatively young field in algebraic topology. Tools from computational topology have proven successful in many scientific disciplines, such as fluid dynamics, biology, material science, climatology, etc. In this talk, we will give a brief introduction to computational topology, focusing primarily on persistent homology. Applications to various datasets from cell biology and climatology will be presented to illustrate the methods.
Thursday, February 23, 2:30 pm
Newton 203
Sedar Ngoma, Auburn University, AL
RECOVERING A DIFFUSION COEFFICIENT IN A PARABOLIC EQUATION ARISING IN GEOCHRONOLOGY
We investigate a problem with applications in geochronology, a branch of geology in which the dating of rock formations and geological events are studied. In particular, we reconstruct the temperature history of rocks. Reconstructing the temperature history amounts to solving (and approximating solutions of) a time-dependent inverse diffusion coefficient problem for a parabolic partial differential equation with an integral constraint. We describe both the direct and the inverse problems, and under some condition, we show that the underlying problem applies to problems of continuous compounding of interest, population dynamics, and radioactive decay. We present some computations and several numerical experiments.
Friday, January 27, 3:00-4:00pm
Newton 203
Cesar Aguilar, SUNY Geneseo
THE PAGERANK ALGORITHM: THE MATHEMATICS BEHID GOOGLE'S SEARCH ENGINE AND ITS APPLICATIONS
In 1998, two graduate students from Stanford changed the way all of us search on the web by creating the search engine Google. Before 1998, search engines used mostly traditional text processing to find and display relevant pages after a search query. The founders of Google had a different idea: Why not model the web as a directed graph and compute the dominant eigenvector of the Google web-matrix to rank all web pages and incorporate this ranking when displaying search results? As you may verify for yourself by looking up the present market value of Google, this idea worked extremely well. In this talk, we will give an overview of Google's PageRank algorithm, some of its applications other than web page ranking, and some of the computational issues involved.
Fall 2016
Wednesday, November 16, 2:30-3:45pm
Newton 202
Jeff Johannes and Gary Towsley, SUNY Geneseo
A CONCISEHISTORY OF CALCULUS
A lively overview of over two thousand years of calculus history. Not only who-did-what along the way, but the cultural and sociological causes and effects of the calculus. Strongly recommended for anyone who has taken or is taking calculus.
Wednesday, November 2, 2:30-3:30pm
Newton 203
Sean Nixon, SUNY Geneseo
OVERTHINKING IT: THE UNNECESSARY APPLICATION OF ADVANCED MATHEMATICS TO POPULAR CULTURE
Part 1: Modeling Politics in Marvel’s Civil War – In the 2016 film, Captain America: Civil War, the Marvel Cinematic Universe moved from the basic her vs. villain plot to a hero vs. hero story. The battle between good and evil to a philosophical debate over the proper level of government oversight. Understanding the politics involved in the Marvel Civil War takes us from one dimensional models and basic game theory to embedded manifolds and applications for computer visualization.
Part 2: Fractional Characterization in Inside Out – Writing a well rounded character is a lot like measuring the coast of Britain, or at least, that’s what Pixar’s Inside Out seems to be telling us. The Anthropomorphic personifications of Riley’s emotions give the audience a simplified representation for the struggles in a young girl’s coming of age. But, they also give a window into how the study of fractional geometry and fractals can help us understand emotional complexity.
Thursday, October 20, 4:00-4:50pm
Newton 204
Alex Rennet, University of Toronto, Mississauga
INCOMPLETENESS, HERCULES AND THE HYDRA
In this talk, I'll start with an introduction to Godel's Incompleteness Theorems. These theorems were a major turning point for our modern understanding of the logical underpinnings of mathematics. One of them can be phrased as follows: "Given any reasonable set of axioms for number theory, there are number-theoretic statements which are true but unprovable from those axioms." In the classic proofs of this theorem, a true but unprovable statement is constructed, called a 'Godel sentence'. However, such classically-constructed Godel sentences didn't seem to have any concrete mathematical meaning. This lead many to wonder whether there were any examples of natural, contentful statements about number theory which are both true and unprovable, like Godel sentences. A number of different positive answers were found. I will discuss my favorite, which involves Hercules and The Hydra fighting to the death, and some really, really large numbers. No particular background knowledge is required, but some basic knowledge of sets and axioms would be helpful.
Thursday, September 22, 4:00-4:50pm
Newton 204
Hossein Shahmohamad, RIT
GRAPH COLORINGS & CHROMATIC POLYNOMIAL: EQUIVALENCE, UNIQUENESS, ROOTS & MORE
This talk will introduce vertex colorings as well as the celebrated chromatic polynomial, which counts the number of proper vertex colorings of a graph given n colors. The chromatic polynomial was intended as a tool to solve the four color conjecture in the early 1900’s. Many interesting properties of this polynomial will be discussed. After introducing graph isomorphism, chromatic equivalence and chromatic uniqueness will be presented. Some open problems in this area will be discussed as well.
Spring 2016
Friday, January 29, 3:00-3:50pm
Newton 204
Arunima Ray, Brandeis University (SUNY Geneseo, Class of 2009)
IS THE SET OF KNOTS FRACTAL?
Knots are everywhere - in your shoelaces, neckties, and usually your earphones. The field of knot theory is devoted to the study of questions like: Are there infinitely many knots? When are two knots the same? How can we tell if one knot is more or less knotted than another? I will discuss the basics of knot theory along with a family of natural functions on the set of all knots. We will then investigate a recent conjecture that this family of functions gives the set of knots (modulo an equivalence relation) the structure of a fractal.
Monday, February 22, 4:00-4:50pm
Newton 201
Cesar Aguilar, California State University at Bakersfield
CONTROLLABILITY OF GRAPHS
Graph theory is an increasingly useful tool to model and analyze coupled dynamic systems in the sciences and engineering. Examples include communication satellites, social interaction sites like Facebook and Twitter, biological processes such as yeast protein interactions and gene regulatory networks, and many others. In this talk, I will present how algebraic graph theory is being used to analyze the ability to control these networked coupled systems.
Tuesday, March 1, 4:00-4:50pm
Newton 214
Kristopher Lee, Iowa State University
THE EIGENVALUE MACHINE
Suppose that you walk into the Fraser Study Area and find that a strange machine has been installed. It asks you to input a matrix. So, you give it one, it shakes and rattles a bit, and then it gives you a new matrix. Curious, you inspect the device and find the following message: "This machine is linear and it does not change eigenvalues." Is this enough information to figure out how the machine works? Come and find out the answer! Along the way, we will discuss the history of such machines, the current ones being studied, and their use in quantum computing.
Physics Department Colloquium
Thursday, March 3, 4:00-4:50pm
Newton 214
Gary Towsley, SUNY Geneseo
MATHEMATICAL PHYSICS AND THE SCIENTIFIC REVOLUTION
The change in both the nature and the content of the natural sciences beginning with Copernicus' consideration of a different underlying dynamic for the motions of the heavenly bodies to the culmination of the process in Newton's Principia has been called the "Scientific Revolution". In recent years the concept of the "Scientific Revolution" has come under attack by historians and philosophers of science (and others). The chief criticism is that the accepted story of the revolution is far too simple. A major component of the scientific revolution was the alteration in the way mathematics was used in science, particularly in Physics. Newton and Galileo were two of the principle figures in this revolution but the way they each used mathematics was very different and often at odds with the accepted story of the revolution. This talk will deal with just how each of these figures used mathematics in advancing a new Physics.
Friday, March 4, 2:30-3:20pm
Newton 201
Min Wang, Equifax Inc.
INTRODUCTION TO BOUNDARY VALUE PROBLEMS: FROM INTEGER TO FRACTION
Boundary value problem is an important topic in differential equation theory and has been a focus of research for decades. In this talk, some basic concepts, approaches, and challenges in this area will be presented. Potential research projects for students, especially undergraduate students, will be discussed as well. This talk will be appropriate for undergraduate students and graduate students who have an interest in differential equations.
Wednesday, March 30, 3:30-4:20pm
South 328
Walter Gerych, SUNY Geneseo PRISM
REU TALK
My team, under the mentorship of Kansas State's Dr. LeCrone, worked to develop a method of approximating Mean Curvature Flow with obstacles in the plane using cellular automata. Mean curvature flow is a well understood type of geometric flow of surfaces. However, when obstacles are placed in such a way as to obstruct the flow of the surfaces the system is no longer easily understood analytically. To study flow with obstacles, we developed a discrete model of such flow using cellular automata. Cellular automata are grids of discrete cells in which each cell can take on one of a finite number of states. The cells then transition to different states in "generations" over discrete time steps. Our goal was to develop updating rules in such a way that the cells would model mean curvature flow.
Wednesday, April 6, 3:30-4:20pm
South 328
Stephanie Allen, SUNY Geneseo PRISM
REU TALK
Identifying those groups in economic need is a process that can be approached in several different ways. For the county of Arlington, Virginia – one of the wealthiest counties in the US – I undertook two analyses to accomplish this goal. In the first, I looked at household-level Census data and ran a series of confidence intervals with the intent to find which household groups were overrepresented (and underrepresented) in the bottom portion of the income distribution. Group descriptors included racial composition of households, household language, veteran status, etc. In the second analysis, I examined Census tract-level data and used factor analysis (a statistical method that finds patterns in data) to rank the tracks of Arlington County by economic prosperity. I identified the tracts at the bottom of this ranking and sought to discover which groups of individuals (using the same characteristics as in the first analysis) were overrepresented in these tracts. Therefore, one analysis approaches the important question of ‘who is in economic need?’ from a micro point of view, while the other analysis approaches this question from a more macro point of view.
Thursday, April 7, 4:00-4:50p
Newton 203
Amanda Tucker, University of Rochester
MULTIPLE ZETA VALUES
What's the difference between 3, 1/3, the sum from n=1 to infinity of 1/n^3, and pi? We will start with a discussion of what it means for a number to be integral, rational, algebraic, or transcendental. We will talk about the history of the multiple zeta values (certain real numbers) and some open problems about them. You will leave this talk knowing more about the real numbers than you thought was possible, but also with more questions about the real numbers than you thought was possible! Some familiarity with vector spaces and geometric series will help, but by no means is necessary for getting something out of this talk. A deck of cards will be involved.
Thursday, April 14, 3:30-4:20pm
South 328
Megan Brunner, SUNY Geneseo PRISM
REU TALK
This research is a reflection of the need for education to prepare students for either careers or college. As the world is becoming increasingly more globalized, it is more necessary for high school graduates to have basic understandings of other cultures and subcultures. We worked with three middle schools in Connecticut that are implementing interdisciplinary units that have components of multicultural knowledge, building "intercultural competence," or ICC, in their students. I worked to develop assessment tools for these teachers and school districts. The tools will measure specific qualities we determined to show "high ICC levels" in middle school students. There is a strong theoretical background influencing these decisions and the creation of the tools, which have multiple uses within classroom environments to gain a comprehensive understanding of the students' skills.
Megan will also introduce the research she did the previous summer at Kansas State University that focused on graph theory and combinatorial optimization.
Wednesday, April 27, 2:45-3:35pm
Newton 204
Brendan Murphy, University of Rochester (SUNY Geneseo, Class of 2010)
THE SUM-PRODUCT PROBLEM
Erdos and Szemeredi conjectured that for a finite sequence of integers a1 < a2 < ... < an, the number of integers of the form ai+aj,aiaj, 1 = i = j = n is more than n2-e for any e > 0. This is known as the "sum-product problem".
Despite three decades of effort, this conjecture is far from being resolved. In fact, work on the sum-product problem and related problems has grown into a field known as "arithmetic combinatorics", which combines elements of combinatorics, number theory, and algebra.
We will place the sum-product conjecture in context and examine the evidence that led Erdos and Szemeredi to pose their conjecture, as well as survey partial progress, variations, and generalizations. Along the way we will see a few gems, including Erdos' "multiplication table theorem", which answers the question "How many distinct entries are in an n by n multiplication table?". If time permits, we will discuss applications of sum-product type results to theoretical computer science.
This talk will be accessible to anyone who knows algebra and coordinate geometry. However, knowledge of sets, limits, and experience with proofs may be helpful.