Projectile Scattering Experiment

 Supported in part by the National Science Foundation (Grant No 1439762). The opinions, findings, and conclusions or recommendations expressed are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Question: How can physicists learn about targets by measuring the way that projectiles scatter from them?

Motivation and Introduction

 

  In particle accelerators all over the world, physicists scatter particles from targets and look at how the particles scatter at different angles.  Using information like this they've learned about the size of the atomic nucleus, the types of elements making up a sample, and they've even discovered new subatomic particles!

  In this lab activity we will fire Nerf projectiles at a cylindrical target using a toy launcher, count the number of projectiles that scatter into detectors placed at different angles, and determine the radius of the target from that information.

By the way, this is an updated version of a scattering experiment that was popular in the 1960s and 1970s using BBs.  For example, see

Robert Jasinski and Jeffrey Weitz, “Apparatus for Teaching Physics: Sargent-Welch Scattering Apparatus, an Evaluation,” The Physics Teacher 12, 305-306 (1974).

D. J. Prowse, “Note on the ‘Welch” Scattering Apparatus,” American Journal of Physics 29, 854-855 (1961).

Robert I. Price,  “Use of the ‘Welch’ Scattering Apparatus,” American Journal of Physics 55 931-932 (1987).

Setting up the Apparatus

 

 

 

Deriving the Scattering Cross Section Formula

Like billiard balls on a pool table, the projectiles will bounce off the target so that the angle of incidence is equal to the angle of reflection.  We can use this fact to derive an formula to predict the number of projectiles that will scatter at different angles.  See how in the video below.

In the formula below, dN represents the number of projectiles detected at a particular angle θ, N is the total number of projectiles, x is the range of impact parameters, r is the radius of the projectile, and dθ is the angular size of the detector.  We will determine the  value for R, the radius of the target, that best fits this theoretical curve to the experimental scattering data.

Collecting the Scattering Data

Here's a description of our data collection method. Notice that we were careful to fire the same number of projectiles from each impact parameter value.

As this video shows, projectiles with small impact parameters scatter to large scattering angles and those with large impact parameters scatter to small scattering angles.

Analysis and Results for the One-Gallon Paint Can Target

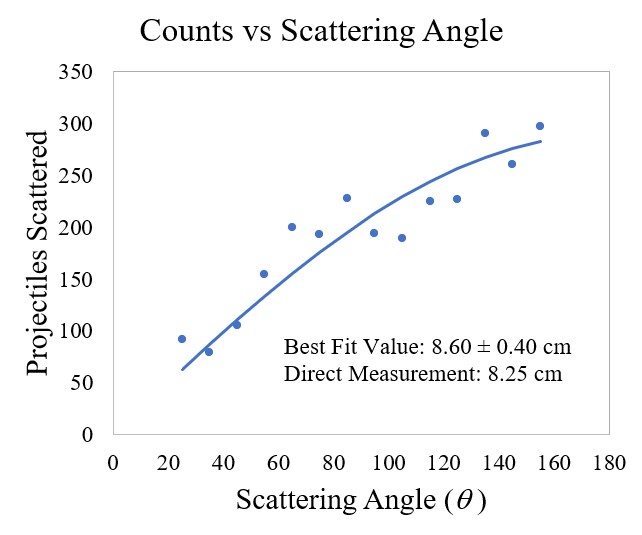
For the gallon paint can target, we used the Solver feature in Microsoft Excel to determine the best-fit value for the target radius.  Our scattering experiments gave a best-fit value of 8.60 ± 0.40 cm, which is consistent with the measured value of 8.25 cm! 

The scattering measurement correctly determined the radius of the target!

Finding the Radius for a Different Target - A Do-it-Yourself Activity!

 

We collected scattering data for a second target that has a different radius.  For this experiment, the projectile radius (r) was 1.1 cm.  The range of the impact parameters (x) was 5 cm.  The total number of particles detected (N) was 2618.

Here are the data for the second target:

Plot these data (Counts vs. Angle) and construct the theory curve, using

Make some guesses about the Target radius (R) and see what value of R gives you the best fit.

Materials

• Our projectile launcher is a Nerf Rival Nemesis MXVII-10K, which is battery operated
• Our scattering chamber is a 160-cm diameter foldable dog pool that is 30 cm high
• Our (first) target is a one-gallon paint can
• Our detector bags are made from a fleece blanket and supported by a wire frame. 

Below are the dimensions for the wire frames.